Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 63
Para o circuito da Figura , determine o valor de
Passo 1
Galera, vamos começar passar a configura marcada na figura abaixo para .
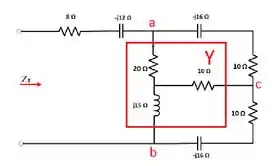
O nosso circuito agora assume uma nova cara,
Passo 2
O segundo passo agora é olhar para as duas malhas que surgiram, que estão mostradas na figura abaixo. Vamos agora encontrar os equivalentes dessas duas malhas:
Desse modo, o circuito fica da seguinte forma:
Passo 3
Seja o equivalente entre os nós e . O valor dele é o resultado de em paralelo com :
Por fim, a impedância é a combinação em série de com o resistor e com o capacitor de :
Resposta
A impedância é igual a:
Exercícios de Livros Relacionados
a) Mostre que, a uma dada frequência ω , os circuitos na Figura P9.20(a) e (b) terão a mesma impedância entre os terminais a,b se R 1 = R 2 1 + ω 2 R 2 2 C 2 2 C 1 = 1 + ω 2 R 2 2 C 2 2 ω 2 R 2 2 C 2
a) Usando os valores dos componentes do apêndice H, determine um único capacitor ou uma rede de capacitores que, quando combinados em paralelo com o circuito RL do Problema 9.26(a), resulta em uma imp
a) Para o circuito mostrado na Figura P9.24, determine a frequência (em radianos por segundo) em que a impedância Z a b é puramente resistiva. b) Determine o valor de Z a b na frequência determinada n
Determine a impedância Z a b no circuito da Figura P9.22. Expresse Z a b em forma polar e também em forma retangular.
a) Mostre que, a uma dada frequência ω , os circuitos na Figura P9.20(a) e (b) terão a mesma impedância entre os terminais a,b se R 2 = 1 + ω 2 R 1 2 C 1 2 ω 2 R 1 2 C 1 2 C 2 = C 1 1 + ω 2 R 1 2 C 1