Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 99
O circuito mostrado na Figura P7.99 é conhecido como um multivibrador astável e encontra ampla aplicação em circuitos de pulso. A finalidade deste problema é relacionar a carga e descarga dos capacitores com o funcionamento do circuito. O segredo para analisar o circuito é entender o comportamento das chaves transistorizadas ideais e O circuito é projetado de modo que as chaves se alternem automaticamente entre o estado LIGADO (ON) e o estado DESLIGADO (OFF). Quando está no estado OFF, está no estado ON e vice-versa. Assim, na análise desse circuito, supomos que uma chave esteja ou no estado ON ou no estado OFF. Também admitimos que uma chave transistorizada ideal possa mudar de estado instantaneamente. Em outras palavras, ela pode passar repentinamente do estado OFF para o estado ON e vice-versa. Quando uma chave transistorizada está no estado ON, (1) a corrente de base é maior do que zero, (2) a tensão terminal é igual a zero e (3) a tensão terminal é igual a zero. Portanto, quando uma chave transistorizada está no estado ON, existe um curto-circuito entre os terminais e . Quando uma chave transistorizada está no estado OFF, (1) a tensão terminal é negativa, (2) a corrente de base é igual a zero, e (3) há um circuito aberto entre os terminais . Sendo assim, quando uma chave transistorizada está no estado OFF, existe um circuito aberto entre os terminais e . Suponha que estivesse ligada e tenha acabado de passar abruptamente para o estado OFF, enquanto estava no estado OFF e acabou de passar repentinamente para o estado ON. Você pode supor que, nessa circunstância, esteja carregado com tensão de alimentação e a carga em seja nula. Admita também que e
a) Determine a expressão para , durante o intervalo em que esteja no estado OFF.
b) Determine a expressão para , durante o intervalo em que esteja no estado OFF.
c) Determine o tempo em que permanece no estado OFF.
d) Determine o valor de ao final do intervalo em que está no estado OFF.
e) Determine a expressão para , durante o intervalo em que está no estado OFF.
f) Determine o valor de , ao final do intervalo em que está no estado OFF.
g) Faça um gráfico de em função de t durante o intervalo em que está no estado OFF.
h) Faça um gráfico de em função de t durante o intervalo em que está no estado OFF.
Passo 1
Faaala, galerinha!! Como vocês estão? Partiu resolver mais uma questãozinha?
Para resolvermos o item (a), devemos primeiramente fazer uma análise do que está acontecendo:
Enquanto estiver ligado, é carregado em , positivo no terminal esquerdo. No instante em que liga, o capacitor é conectado através de assim,
Essa tensão negativa desliga . Agora, a polaridade da tensão em começa a inverter, ou seja, o terminal direito de começa a carregar em direção a , positivo à direita. No instante em que a carga em atinge zero, é zero e liga. Isso faz com que e desliga.
Agora os capacitores e começam a carregar com as polaridades para ligar e desligar . Esta ação de comutação se repete repetidamente enquanto o circuito estiver energizado. No instante em que vira ligado, a tensão que controla o estado de é regida pelo seguinte circuito:
O circuito segue que:
Passo 2
No item (b), enquanto está desligado e está ligado, a tensão de saída é a mesma que a tensão em , assim:
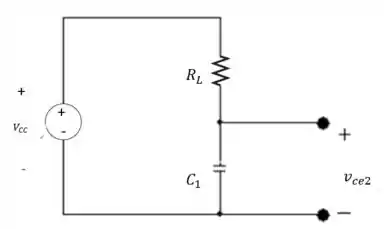
O circuito segue que:
Passo 3
Seguindo para o item (c), vemos que estará desligado até que atinja zero. Assim que for zero, se tornará positivo e ligará .
Assim, quando ou quando
Passo 4
Resolvendo o item (d), observamos que quando está no estado desligado, e nós temos:
Passo 5
Ao analisar o item (e), vemos que antes de ligar, é igual a zero. No instante em que liga, nós temos o seguinte cenário:
Passo 6
Por fim, ao analisar o que ocorre no item (f), concluímos que no instante em que liga de volta, Portanto:
Prontinho, pessoal!! Bora resolver mais uma questão juntos?
Resposta
a)
b)
c)
d)
e)
f)