Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 66

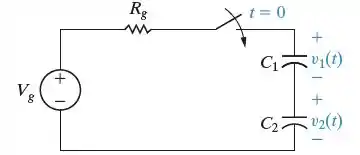
Não há nenhuma energia armazenada nos capacitores C1 e C2 no instante em que a chave é fechada, no circuito visto na Figura P7.66.

  1. Deduza as expressões para v 1 t e v 2 t para t>=0.
  2. Use as expressões deduzidas para em (a) determinar v 1 ∞   e   v 2 ( ∞ ) .

Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre resposta de circuitos RL e RC de primeira ordem!

  1. Deixaremos que i seja a corrente na direção horária pelo circuito, teremos que:

    2. V g = i R g + 1 C e ∫ i d x

    Agora, diferenciando a equação temos que:

    d i d t + 1 R g C e i = 0

    Uma vez que:

    i = V g R g e - t / R g C e → τ = R g C e

    Logo:

    v 1 t = V g C 2 C 1 + C 2 1 - e - t T

    E também:

    v 2 t = V g C 1 C 1 + C 2 1 - e - t T

    Passo 2

  2. Simplesmente resolvemos a relação:

v 1 ∞ = C 2 C 1 + C 2 V g ;

v 2 ∞ = C 1 C 1 + C 2 V g ;

Resposta

  1. v 1 t = V g C 2 C 1 + C 2 1 - e - t T

    E também:

    v 2 t = V g C 1 C 1 + C 2 1 - e - t T

v 1 ∞ = C 2 C 1 + C 2 V g ;

v 2 ∞ = C 1 C 1 + C 2 V g ;

Exercícios de Livros Relacionados

A chave no circuito da Figura P7.53 esteve na posição a por um longo tempo. Em t = 0, ela é colocada na posição b. Calcule (a) a tensão inicial no capacitor; (b) a tensão final no capacitor; (c) a con
A chave no circuito visto na Figura P7.54 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. Para t $ 0+, determine a) vo (t). b) i o (t).
A chave do circuito visto na Figura P7.55 esteve na posição a por um longo tempo. Em t = 0, a chave passa instantaneamente para a posição b. Determine vo (t) e i o (t) para t $ 0+.
A chave do circuito na Figura P7.57 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. No instante em que a chave faz contato com o terminal b, a chave 2 ab
O circuito da Figura P7.56 está em operação por um longo tempo. Em t = 0, a fonte de tensão inverte a polaridade e a fonte de corrente cai de 3 mA para 2 mA. Determine vo (t) para t $ 0.