Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 5.Problemas - Ex. 37

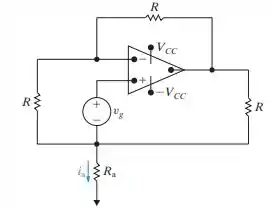
  1. Mostre que, quando o amp op ideal da Figura P5.37 está operando em sua região linear,

    2. i a   = 3 v g R

  2. Mostre que o amp op ideal satura quando

  R a   = R ± V C C   -   2 v g 3 v g

Passo 1

Falaiii meus amores, cêis tão suave?

Bora pra mais uma??

Então, encostaa!!

  1. Aplicando a lei das correntes de Kirchhoff no terminal inversor do op-amp

    2. v n - v a R + v n - v o R = 0

    2 v n - v a = v o                     ( 1 )

    Aplicando a lei das correntes de Kirchhoff no nó que une a fonte de tensão v g e o resistor R a

    v a R a + v a - v n R + v a - v o R = 0

    v a 1 R a + 2 R - v n R = v o R

    v a 2 + R R a - v n = v o               ( 2 )

    Passo 2

    Agora iremos equacionar as equações (1) e a (2)

    2 v n - v a = v a 2 + R R a - v n

    3 v n = v a 2 + R R a + v a

    3 v n = v a 3 + R R a

    Devido ao conceito de terra virtual, a tensão no terminal inversor é igual à tensão no terminal não inversor. Portanto v n = v p = v a + v g . Substituindo este valor na equação acima.

    3 v a + v g = v a 3 + R R a

    3 v a + 3 v g = 3 v a + R R a v a

    3 v g = R R a v a

    v a = 3 v g R a R

    Aplique a lei de Ohm para encontrar a corrente i a

    i a = v a R a

    = 3 v g R a R R a

    = 3 v g R

    Portanto, a corrente i a é igual a 3 v g / R .

    Passo 3

  2. Na saturação v o = ± V c c                 ( 3 )

Devido ao conceito de solo virtual v n = v p = v g + v a

Substitua

2 v g + v a - v a = v o

2 v g + 2 v a - v a = v o

2 v g + v a = v o

v a = v o - 2 v g

v a = ± V c c - 2 v g                 ( 4 )

Passo 2

E da equação (2)

v a 2 + R R a - v n = v o

v a 2 + R R a - v g - v a = ± V c c

2 v a + R R a v a - v a = ± V c c + v g

v a + R R a v a = ± V c c + v g

v a 1 + R R a = ± V c c + v g                   ( 5 )

Dividindo a equação (4) por (5) para resolver R a

v a v a 1 + R R a = ± V c c - 2 v g ± V c c + v g

± V c c + v g ± V c c - 2 v g = 1 + R R a

R R a = ± V c c + v g ± V c c - 2 v g - 1

R R a = ± V c c + v g ∓ V c c + 2 v g ± V c c - 2 v g

R R a = 3 v g ± V c c - 2 v g

R a = R ± V c c - 2 v g 3 v g

Resposta

  1. Portanto, a corrente i a é igual a 3 v g / R .
  2. Portanto, o valor de R a é igual a

R ± V c c - 2 v g 3 v g

Exercícios de Livros Relacionados

Calcule V.
Calcule v se v_g = 4 cos 6 t V
Calcule v se v g = 8 cos ⁡ 3 tV . (Sugestão: Note que v 1 = v / μ , onde μ = 2 é o ganho da FTCT.)
Empregue o método do Prob. 3.17 para construir uma resistência negativa de -6Ω, onde a potência dissipada em R 1 é 2W quando v 1 = 6 V .
Se Rf = R1 = 1 k Ω no circuito do Prob. 3.29, calcule os valores dos demais resistores de forma que Vo = V1 + V2. (Note que o resultado é verdadeiro se R = Rf = R1 = R2.)