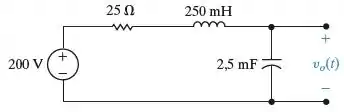
O circuito mostrado na Figura P8.53 esteve em funcionamento por um longo tempo. Em t = 0, a tensão da fonte cai repentinamente para 150 V. Determine vo(t) para .

Temos que:

Em outubro de 1745, Ewald Georg von Kleist, descobriu que uma carga poderia ser armazenada, conectando um gerador de alta tensão eletrostática por um fio a uma jarra de vidro com água, que estava em sua mão.[1] A mão de Von Kleist e a água agiram como condutores, e a jarra como um dielétrico (mas os detalhes do mecanismo não foram identificados corretamente no momento). Von Kleist descobriu, após a remoção do gerador, que ao tocar o fio, o resultado era um doloroso choque. Em uma carta descrevendo o experimento, ele disse: "Eu não levaria um segundo choque pelo reino de França".[2] No ano seguinte, na Universidade de Leiden, o físico holandês Pieter van Musschenbroek inventou um capacitor similar, que foi nomeado de Jarra de Leiden.[3]