Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.2 - Ex. 3
Um circuito está em regime permanente em e a chave é mudada da posição 1 para a posição 2 em . Calcule para .
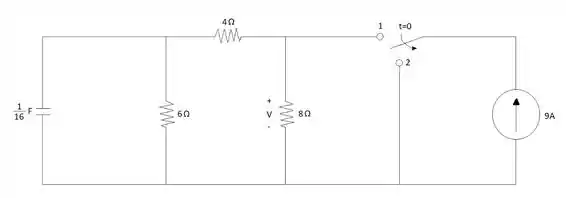
Passo 1
Olá galerinha, tudo bem? Espero ajudar vocês nesta questão, vamos lá.
De acordo com os dados fornecidos pelo enunciado da questão o circuito está em regime permanente quando e a posição da chave está no ponto 1, isso quer dizer que com essa configuração do circuito o capacitor se comporta como um circuito aberto e há participação da fonte de corrente de 9 A.
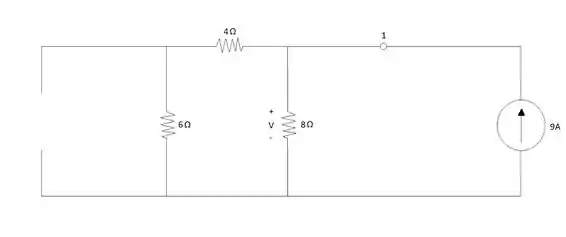
Neste primeiro momento temos que descobrir quanto vale a tensão do capacitor, já que essa tensão não irá mudar quando a chave ficar na posição 2, e dessa forma poderemos descobrir quanto vale a tensão do resistor de 8 Ω quando .
Sendo assim podemos prosseguir os cálculos para encontrar o valor da tensão do capacitor que é a mesma tensão do resistor de 6 Ω. Para isso encontramos primeiro a resistência equivalente do circuito e a sua respectiva tensão:
Com esses valores encontrados calculamos a tensão do resistor de 6 Ω usando o divisor de tensão:
Essa tensão seria a tensão inicial do capacitor.
Passo 2
Para encontrar a tensão do resistor de 8 Ω é preciso colocar a chave na posição 2 e analisar o circuito novamente com essa configuração. Desta vez o capacitor se comporta como o fornecedor de energia no circuito e a tensão dele é escrita da seguinte forma:
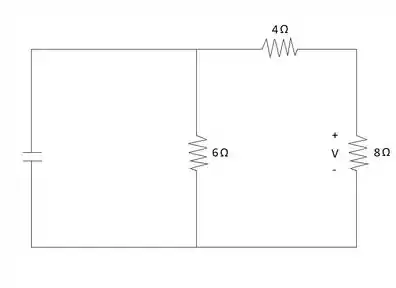
Dito isso, é preciso encontrar a resistência equivalente do circuito quando e assim usar no cálculo de divisor de tensão que será utilizado para encontrar a tensão que a questão pede:
A constante de tempo fica:
Dessa forma, substituindo os valores encontrados na expressão da tensão num capacitor temos:
Passo 3
Finalmente aplica-se o divisor de tensão no circuito para encontrar a tensão do resistor de 6 Ω:
Resposta