Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 28
Determine para .
Passo 1
: a tensão vai ser igual a 15 V, sem mistérios nem nada, vai ser exatamente igual ao da fonte de tensão.
: Só sobra o resistor de e a fonte controlada, então vamos usar Thévenin para descobrir qual a tensão e a resistência, parte bem simples também
E para a resistência equivalente:
Passo 2
O circuito equivalente fica desse jeito aqui:
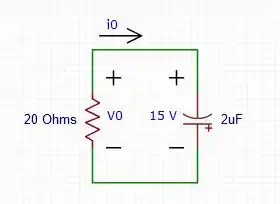
Já temos todas as ferramentas para calcular a constante de tempo e a equação da tensão no capacitor:
Logo,
Passo 3
A corrente é a tensão dividido pela resistência equivalente, é isto!
Resposta
Exercícios de Livros Relacionados
A forma de onda de tensão mostrada na Figura P7.84 (a) é aplicada ao circuito da Figura P7.84(b). A corrente inicial no capacitor é igual a zero.Calcule v 0 ( t ) .Faça um gráfico de v 0 t em função d
A fonte de tensão no circuito da Figura P7.83(a) está gerando o sinal mostrado na Figura P7.83(b). Não há nenhuma energia armazenada em t=0.Determine as expressões para v 0 ( t ) que sejam válidas par
Calcule v para t0 se não existe energia inicial armazenada.
Calcule o valor ou a faixa de valores de μ = 1 + R ≥ 1 tal que o circuito seja:a) superamortecido;b) subamortecido;c) amortecimento crítico;
a) Calcule v para t0 , se v a 0 = 0 e v b 0 = 2 V .b) Repita a parte (a) se a fonte de 4 - V e trocada por uma de 26 cos 2 t V . c) Repita a parte (a) se a fonte de 4 - V foi substituída por uma de