Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 7.Problemas - Ex. 21

A chave no circuito da Figura P7.21 esteve na posição esquerda por um longo tempo. Em t = 0, ela passa para a posição direita, onde permanece. a) Determine a queda de tensão inicial no capacitor. b) Determine a energia inicial armazenada pelo capacitor. c) Determine a constante de tempo do circuito para t . 0. d) Escreva a expressão para a tensão do capacitor v(t) para t $ 0.

Passo 1

[a] – Para t < 0 :  

O capacitor se comporta como um circuito aberto, dado o fato de estar muito tempo em um determinado estado, logo não passa corrente por ali, então, a tensão fica no circuito fechado entre a fonte e o resistor.

Calculando v 0 , temos:

v 0 = 20000 0.01 = 200   V  

Passo 2

[b] – Para o cálculo da energia inicial, a informação da tensão é utilizada, como já temos, vamos calcular!

Lembrando da fórmula w 0 = 1 2 C v 0 2 , temos o seguinte resultado:

w 0 = 1 2 400 × 10 - 9 200 2

Fazendo alguns cálculos, temos:

w 0 = 8   m J

Passo 3

[c] – Para t > 0 , o circuito tem essa característica:

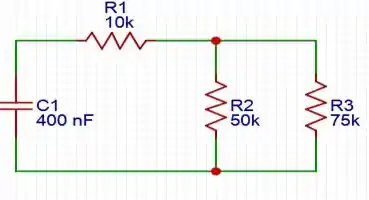
Logo, para resistência equivalente por exemplo, basta fazer o paralelo dos resistores de 50   k Ω e 75   k Ω , e depois, fazer em série com o resistor de 10   k Ω .

R e q = 10000 + 50000 × 75000 50000 + 75000

Logo, a resistência equivalente é igual a:

R e q = 40   k Ω

Para o cálculo da constante de tempo, basta multiplicar essa resistência com o valor do capacitor. Dessa forma

τ = R e q C = 40000 400 × 10 - 9 = 16   m s

Passo 4

[d] – Para encontrar a equação da tensão neste circuito RC, basta substituir os valores:

v t = v 0 e - t / τ ,         t ≥ 0

Calculando o inverso da constante de tempo:

1 τ = 62.5

Com isso, temos:

v t = 200 e - 62.5 t   V ,     t ≥ 0

Resposta

a )   v 0 = 200   V  

b )   w 0 = 8   m J

c )   τ = 16   m s  

d )   v t = 200 e - 62.5 t   V ,     t ≥ 0

Exercícios de Livros Relacionados

Projete um circuito com amplificador operacional tal que v 0 = 10 ⋅ v s + 2 ⋅ ∫ v s d t Onde v s e v 0 são, respectivamente, a tensão de entrada e a de saída.
Um circuito R C possui R = 2 Ω e C = 4F . A constante de tempo é: a0,5s b2s c4s d8s e15s
Um capacitor em um circuito R C com R = 2 Ω e C = 4F está sendo carregado. O tempo necessário para a tensão no capacitor atingir 63,2 % de seu valor em regime estacionário é: a2s b4s c8s d16s en e n h
Determine a constante de tempo para o circuito R C da figura 7.82.
Supondo que a chave na figura 7.87 se encontra na posição A há um longo período e seja mudada para a posição B em t = 0 . Em seguida, tem t = 1s , a chave se move de B para C . Determine v c t para t