Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 44

No circuito o transformador ideal da Figura 13.109 , determine i 1 ( t ) e i 2 ( t ) .

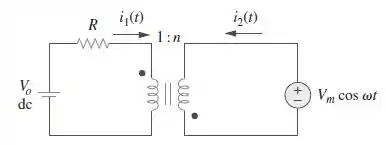
Passo 1

Pessoal, nós podemos aplicar o princípio da superposição para encontrar as correntes i 1 ( t ) e i 2 ( t ) . Seja i 1 t = i 1 d t + i 1 a ( t ) e i 2 t = i 2 d t + i 2 a ( t ) onde i 1 d ( t ) e i 2 d ( t ) são provenientes da fonte de corrente contínua e i 1 a ( t ) e i 2 a ( t ) são da fonte de corrente alternada. Vamos considerar a fonte DC primeiro:

Para a malha 1 ,

V 0 = I 1 d R   →     I 1 d = V 0 R

Para a malha 2 ,

I 2 d = 0

Isso acontece porque uma fonte dependente do tempo é necessária no primário do circuito para induzir tensão/corrente no secundário.

Passo 2

Agora, vamos considerar a fonte AC. Aplicando a lei das malhas na malha esquerda, temos:

0 = I 1 a R + V 1   →     V 1 = - I 1 a R … ( 1 )

Similarmente, aplicando a lei das malhas na malha da direita:

V 2 = V m … ( 2 )

Nos terminais do transformador, temos:

V 2 V 1 = - n   →     V 2 = - n V 1 … ( 3 )

I 2 a I 1 a = 1 n … ( 4 )

Passo 3

Substituindo as equações ( 1 ) e ( 2 ) na equação ( 3 ) ,

V m = - n - I 1 R = n I 1 a R

Além disso,

I 1 a = V m n R

E da equação ( 4 ) :

I 2 a = 1 n I 1 a = V m n 2 R

No domínio do tempo,

i 1 a t = V m n R cos ⁡ ω t

i 2 a t = V m n 2 R cos ⁡ ω t

Passo 4

Por fim, as correntes totais são:

i 1 t = i 1 d t + i 1 a t = V 0 R + V m n R cos ⁡ ω t

i 2 t = i 2 d t + i 2 a t = 0 + V m n 2 R cos ⁡ ω t

Resposta

As correntes são iguais a:

i 1 t = i 1 d t + i 1 a t = V 0 R + V m n R cos ⁡ ω t

i 2 t = i 2 d t + i 2 a t = 0 + V m n 2 R cos ⁡ ω t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um transformador com quatro enrolamentos (Figura 13.146) é usado normalmente em equipamentos (por exemplo, PCs, VCRs) que podem operar tanto em 110V como em 220V . Isso torna esse equipamento adequado
Dez lâmpadas em paralelo são alimentadas por um transformador de 7.200 / 120V , conforme indicado na Figura13.147, na qual as lâmpadas são representadas em termos de modelo por resistores de 144Ω Dete
Alguns sistemas modernos de transmissão de energia elétrica agora têm maiores segmentos de transmissão com altas tensões CC. Existem várias boas razões para isso, mas não vamos analisá-lo nesse moment
No circuito da Figura 13.124, faça v s = 40c o s1.000 t . Determine a potência média liberada para cada resistor.
Observe o circuito da Figura 13.125 da próxima página. (a) Determine as correntes I 1 ,I 2eI 3 . (b) Determine a potência dissipada no resistor de 40Ω .