Alguns sistemas modernos de transmissão de energia elétrica agora têm maiores segmentos de transmissão com altas tensões CC. Existem várias boas razões para isso, mas não vamos analisá-lo nesse momento. Para converter de CA para CC, são usados circuitos eletrônicos de
potência. A tensão CA trifásica inicial é retificada (usando um retificador de onda completa). Verifica-se que o secundário conectado em uma combinação triângulo-estrela e triângulo-triângulo proporcionam uma ondulação (ripple) muito menor após o retificador de onda completa. Como isso ocorre? Lembre-se de que esses são dispositivos reais e são enrolados em núcleos comuns.
Sugestão: Use as Figuras 13.47 e 13.49 e o fato de que cada bobina do secundário conectado em estrela e cada bobina do secundário conectado em triângulo estão enroladas no mesmo núcleo de cada bobina do primário conectada em triângulo de modo que a tensão de cada uma das bobinas correspondentes estão em fase. Quando os terminais de saída do secundário são conectados à carga através de retificadores de onda completa, vemos que a ondulação é bastante reduzida. Caso necessário, consulte seu professor para mais orientações.
Passo 1
Esse é um problema muito interessante e muito prático.
Você está criando um segundo conjunto de ondas senoidais para enviar pelo retificador de onda completa, 30 ° defasado do primeiro conjunto. Começamos mostrando os componentes do transformador.
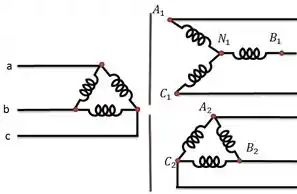
Passo 2
O caminho aqui é enrolar as bobinas secundárias com cada fase da primária. Assim, a-b é enrolado em torno do mesmo núcleo que e .
Passo 3
A próxima coisa que precisamos fazer é garantir que as tensões sejam iguais. Precisamos trabalhar o número de voltas de cada secundário para que o pico de seja igual a .
Agora, vejamos algumas das equações que envolvem. Se deixarmos
assuma que temos um transformador ideal, e as relações de espiras são tais que obtemos
e
Passo 4
Em seguida, vejamos
Isso leva a
Passo 5
agora precisa determinar
Isso faz com que a tensão de saída por fase seja igual a
Passo 6
Podemos fazer isso para cada fase e terminar com a saída sendo enviada ao retificador de onda completa.