Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 49
Determine a corrente no circuito do transformador ideal da Figura .
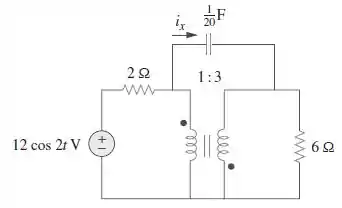
Passo 1
Galerinha, primeira coisa que precisamos fazer é transformar os elementos do circuito para o domínio da frequência.
O circuito fica da seguinte maneira:
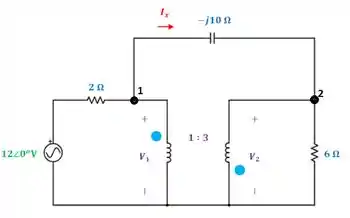
Passo 2
Vamos aplicar a lei dos nós no nó 1:
Similarmente, aplicando a lei dos nós no nó 2:
No terminal do transformador, temos que:
Passo 3
Substituindo as equações e em e :
Se somarmos as duas equações, vamos ter:
A corrente pode ser calculada através da divisão da diferença de potência entre os nós 1 e 2 e a reatância:
Passando para o domínio do tempo:
Resposta
A corrente é igual a:
Exercícios de Livros Relacionados
Use o conceito de impedância refletida para determinar a impedância de entrada e a corrente I 1 na Figura 13.116 .
No circuito o transformador ideal da Figura 13.109 , determine i 1 ( t ) e i 2 ( t ) .
Observe o circuito da Figura 13.118 .Determine n para a máxima potência fornecida para a carga de 200Ω .Determine a potência na carga de 200Ω se n = 10 .
Considere a Figure 13.113 e elabore um problema para ajudar outros estudantes a entender melhor como funciona os transformadores ideais.
Um transformador é usado para casar um amplificador com uma carga e 8Ω , conforme mostrado na Figura 13.119 . O equivalente de Thevenin do amplificador é: V t h = 10V e R t h = 128Ω .Determine a relaç