Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 79

Observe o circuito da figura.

  1. Determine Z e n t ( s )
  2. Aplique fatores de escala K m = 10   e   K f = 100 aos elementos. Determine Z e n t ( s )   e   ω o .

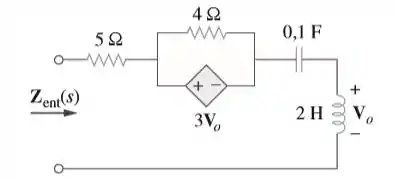
Passo 1

Primeira coisa que vamos fazer é inserir uma fonte de tensão de teste de 1 V entre os terminais e daí teremos esse circuito, já no domínio de Laplace:

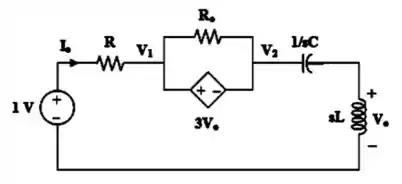
Por causa dessa fonte dependente de tensão, nós temos um supernó e faremos então uma análise nodal.

1 - V 1 R = V 2 s L + 1 s C

Mas como V 1 = V 2 + 3 V o e V o = s L s L + 1 s C V 2

Então, combinando essas duas equações, chegamos em V o em função de V 1 :

V o = s 2 L C 1 + 4 s 2 L C V 1

Agora, substituindo essas equações ( V o = s L s L + 1 s C V 2 e V o = s 2 L C 1 + 4 s 2 L C V 1 ) na primeira da análise nodal, chegaremos em V 1 :

V 1 = 1 + 4 s 2 L C 1 + 4 s 2 L C + s R C

Passo 2

Agora, vamos querer achar I o para então acharmos Z e n t no domínio de Laplace:

I o = 1 - V 1 R = s R C R ( 1 + 4 s 2 L C + s R C )

E então temos:

Z e n t = 1 I o = 1 + s R C + 4 s 2 L C s C = 4 s L + R + 1 s C

Substituindo os valores dos elementos passivos que temos, chegamos em:

Z e n t ( s ) = 8 s + 5 + 10 s

Passo 3

Na letra b nós queremos encontrar os valores de R 1 ´ ,   R 2 ´ ,   L ´   e   C ´ . Sabendo que K m = 10   e   K f = 100 . Então, vamos utilizar a seguinte fórmula:

Para o resistor 1:

R 1 ´ = K m R 1

R 1 ´ = 40 Ω

Para o resistor 2:

R 2 ´ = K m R 2

R 2 ´ = 50 Ω

Para o indutor:

L ´ = K m K f L

L ´ = 0.2 H

Para o capacitor:

C ´ = C K m K f

C ´ = 1 0 - 4 F

Então, nosso Z e n t ( s ) = 0.8 s + 50 + 1 0 4 s

E agora, a frequência de ressonância:

ω o = 1 2 L C = 111.8   r a d / s

Resposta

  1. Z e n t ( s ) = 8 s + 5 + 10 s
  2. Z e n t ( s ) = 0.8 s + 50 + 1 0 4 s

ω o = 1 2 L C = 111.8   r a d / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine v ( t ) para t0 no circuito da figura.
Calcule as correntes de malha no circuito da figura. Apresente seus resultados no domínio s.
Determine i ( t ) para t0 no circuito da figura.
Para o circuito da figura, calcule i ( t ) para t0 .
Considere a figura e elabore um problema para ajudar outros estudantes a entender melhor como usar o teorema de Thévenin (no domínio s) para ajudar na análise de circuito.