Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 43

Considere o circuito da Figura 7.110. Determine i ( t ) para t <   0 e t > 0 .

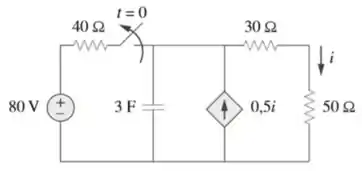
Passo 1

Questão bem tranquila galera, nada desafiador para a gente! Analisando, antes de t   =   0 , o circuito atingiu o estado estacionário para que o capacitor atue como um circuito aberto. O circuito é equivalente ao mostrado na figura abaixo após a transformação da fonte de tensão.

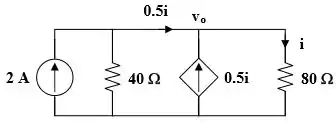
Logo, temos que:

0.5 i = 2 - v 0 40

i = v 0 80

Logo,

1 2 V 0 80 = 2 - V 0 40       →       V 0 = 320 5 = 64   V  

i = V 0 80 = 0.8   A

Passo 2

Agora vamos determinar o que acontece depois de t = 0 . O circuito vai se transformar nisso:

v c t = v c 0 e - t / τ

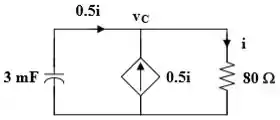
Logo, aplicaremos Thevenin para achar a resistência!

τ = R t h C

Passo 3

Para achar o R t h , vamos substituir o capacitor com uma fonte de 1V, como mostra a figura abaixo:

i = v c 80 = 1 80 A

  i 0 = 0.5 i = 0.5 80 A

Logo,

R t h = 1 i 0 = 80 0.5 = 160   Ω

Daqui a gente já volta pra formula do Tau!!

τ = R t h C = 480

v C 0 = 64   V

v C t = 64 e - t / 480

Voltando para a formula la do inicio:

0.5 i = - i c = - C d v C d t = - 3 1 480 64 e - t / 480  

i t = 800   e - t / 480   m A

Resposta

i t = 800   e - t / 480   m A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine v nas seguintes equações diferenciais, sujeita à condição inicial informada. a d v d t + v = u t , v 0 = 0 V b 2 ⋅ d v d t - v = 3 ⋅ u t , v 0 = - 6
Considere o PSpice ou MultiSim para representar graficamente a amplitude da resposta de frequência do circuito na figura:
Para uma situação de emergência, um engenheiro precisa construir um filtro passa-altas RC. Ele te à sua disposição um capacitor de 10p F , um capacitor de 30p F , um resistor de 1,8k Ω e um resistor d
Para o circuito “tanque” da figura, obtenha a resposta de frequência (tensão no capacitor) usando o PSpice ou MultiSim. Determine a frequência de ressonância do circuito.
Considere o circuito deslocador de fase mostrado na figura e determine H = V 0 / V s