A chave na Figura 7.111 se encontra na posição a há um bom tempo. Em , ela é mudada para a posição . Calcule para todo .
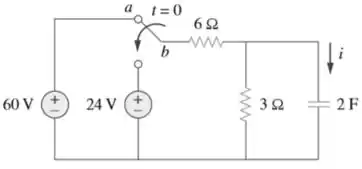
Passo 1
Okay galera, temos aqui um caso em que uma chave alterna entre duas voltagens diferentes, a única diferenca é que ela está em a um bom tempo, fazendo com que o capacitor vire um circuito aberto! Portanto,
E não podemos esquecer de:
Passo 2
Usando a divisão de tensão, temos que
Logo,
Para descobrirmos a corrente, basta utilizarmos a fórmula:
Passo 3
Utilizando-se da formula, temos que: