Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 79

Considere o circuito da figura e determine:

  1. (I_1)/(V_s)
  2. (I_2)/(V_x)

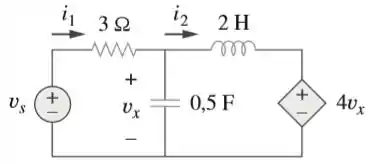
Passo 1

Vamos começar escrevendo I_1 e I_2 usando a primeira Lei de Ohm:

I_1 = (V_s - V_x)/(3)

I_2 = (V_x - 4 V_x)/(2 s)

Como I_2 já está em função somente de V_x , então já podemos achar nossa letra b:

I_2 = (- 3 V_x)/(2 s) -> (I_2)/(V_x) = (- 3)/(2 s)

Passo 2

Agora pra letra a (já que achamos a letra b de cara):

Vamos fazer um LKC no nó:

(V_s - V_x)/(3)_ + (( 0 - V_x ) s)/(2) + (V_x - 4 V_x)/(2 s) = 0

2 s V_s - 2 s V_x - 3 s^2 V_x - 9 V_x = 0

2 s V_s = ( 3 s^2 + 2 s + 9 ) V_x

V_x = (2 s V_s)/(( 3 s^2 + 2 s + 9 ))

Passo 3

Substituindo esse V_x na equação I_1 = (V_s - V_x)/(3) :

3 I_1 = V_s - (2 s V_s)/(( 3 s^2 + 2 s + 9 ))

3 I_1 = (V_s ( 3 s^2 + 2 s + 9 - 2 s ))/(( 3 s^2 + 2 s + 9 ))

(I_1)/(V_s) = (2 s^2 + 9)/(3 ( 3 s^2 + 2 s + 9 )) = (s^2 + 3)/(3 s^2 + 2 s + 9)

E assim achamos a letra a.

Resposta

a) (I_1)/(V_s) = (s^2 + 3)/(3 s^2 + 2 s + 9)

b) (I_2)/(V_x) = (- 3)/(2 s)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A chave no circuito da Figura P13.29 esteve na posição a por um longo tempo antes de passar instantaneamente para a posição b, em t = 0. a) Construa o circuito equivalente no domínio da frequência, pa
No circuito da Figura P13.41, a chave 1 é fechada em t = 0 e a chave do tipo liga-antes-interrompe-depois passa instantaneamente da posição a para a posição b. a) Construa o circuito equivalente no do
a) Determine a corrente no resistor de 160 V no circuito da Figura P13.36. O sentido de referência para a corrente é de cima para baixo, passando pelo resistor.b) Repita a parte (a), se o ponto no enr