Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 13.Problemas - Ex. 41

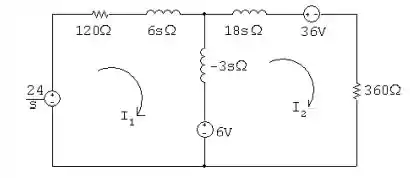
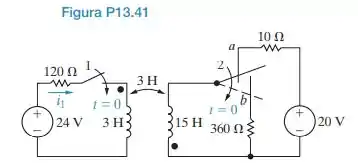
No circuito da Figura P13.41, a chave 1 é fechada em t = 0 e a chave do tipo liga-antes-interrompe-depois passa instantaneamente da posição a para a posição b.

a) Construa o circuito equivalente no domínio da frequência, para t>0.

b) Determine I 1 .

c) Use os teoremas dos valores inicial e final para verificar os valores inicial e final de i 1 .

d) Determine i 1 , para t ≥ 0+.

Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre transformada de Laplace na análise de circuitos!

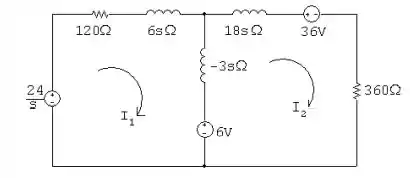
  1. Observando o sistema acima, podemos concluir que o circuito pedido seria da forma seguinte:

  2. Pelo circuito demonstrado, temos que:

    3. 24 s = 120 + 3 s I 1 + 3 s I 2 + 6

    Desenvolvendo esse sistema, precisamos encontrar os valores de ∆   e   N 1 para determinar I 1 . Dessa forma:

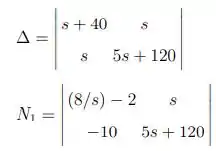
    Logo:

    I 1 = N 1 ∆ = - 50 ( s - 4,8 ) ( s + 20 ) ( s + 60 )

    Passo 2

  3. Já sabemos que:

    4. s I 1 = - 50 ( s - 4,8 ) ( s + 20 ) ( s + 60 )

    Logo:

    lim ⁡ s I 1 = i 1 0 + = 0 A

    lim ⁡ s I 1 = i 1 ∞ = - 50 - 4,8 ( 20 ) ( 60 ) = 0,2 A

  4. Decompondo a expressão de I 1 em termos de K, temos que:

K 1 = 240 1200 = 0,2

K 2 = - 50 - 20 + 240 ( - 20 ) ( 40 ) = 1,35

K 3 = - 50 - 60 + 240 ( - 60 ) ( - 40 ) = 1,35

Portanto:

i 1 t = 0,2 - 1,55 e - 20 t + 1,35 e - 60 t u t A

Resposta

  1. Item a:

  2. Item b:

    3. I 1 = - 50 ( s - 4,8 ) ( s + 20 ) ( s + 60 )

  3. Item c:

    4. lim ⁡ s I 1 = i 1 0 + = 0 A

    lim ⁡ s I 1 = i 1 ∞ = 0,2 A

  4. Item d:

i 1 t = 0,2 - 1,55 e - 20 t + 1,35 e - 60 t u t A

Exercícios de Livros Relacionados

O capacitor no circuito da figura se encontra descarregado inicialmente. Determine v 0 ( t ) para t0 .
A resposta ao degrau de um circuito R L C é dada por d 2 i d t ² + 2 d i d t + 5 i = 10 ² Sabendo que i 0 = 6 e d i 0 d t = 12 , calcule i ( t ) .
Se R = 20Ω , L = 0,6H , qual o valor de C que torna o circuito:a) Superamortecidob) Criticamente amortecidoc) Subamortecido
A resposta ao degrau de um circuito R L C é v = 10 + 20 e - 300 t cos ⁡ 400 t - 2 s e n400 t V ,t ≥ 0 Quando o indutor é 50m H . Determine R e C .
A resposta natural de um circuito RLC é descrita pela equação diferencial d 2 v d t ² + 2 d v d t + v = 0 ² Para a qual as condições iniciais são v 0 = 20V e d v 0 d t = 0 . Determine v ( t ) .