Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 81

Considere o circuito com AOP da figura e determine a função de transferência T ( s ) = I ( s ) V s ( s ) . Considere todas as condições iniciais nulas.

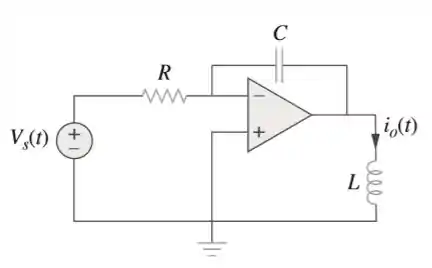
Passo 1

Vamos aqui desenhar esse circuito no domínio de Laplace (domínio s) pra ficar mais claro:

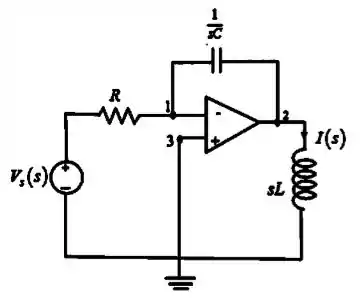
Passo 2

Assumindo que a tensão no nó 1 é V 1 ( s ) , a tensão no nó 2 é V 2 ( s ) e a tensão no nó 3 é V 3 ( s ) , então, aplicando a lei das corrente de Kirchhoff ao nó 1, teremos:

V 1 ( s ) - V s ( s ) R + V 1 ( s ) - V 2 ( s ) 1 s C = 0

V 1 ( s ) [ 1 R + s C ] - s C V 2 ( s ) = V s ( s ) [ 1 R ]

Passo 3

Sabendo que a tensão no terminal positivo é igual ao terminal negativo então a tensão no nó 3 é igual à tensão no nó 1 que é zero.

Substituindo V 1 ( s ) por zero na equação do Passo 2:

V 2 ( s ) = - V s ( s ) s R C

Passo 4

E a tensão no nó 2 será calculada utilizando a primeira Lei de Ohm:

V 2 ( s ) = s L I o ( s )

Substituindo V 2 ( s ) em - V s ( s ) s R C , temos:

I o ( s ) V s ( s ) = - 1 R L C s 2

Então, a função de transferência será:

T ( s ) =   - 1 R L C s 2

Resposta

T ( s ) =   - 1 R L C s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Deduza o par de transformadas dado pela Equação 12.64
Determine a transformada de Laplace (quando P S 0) da derivada da função exponencial ilustrada na Figura 12.8, usando cada um dos dois métodos a seguir:a) Primeiro, diferencie a função e, então, deter
Determine v(t) no Problema 12.26
Os parâmetros do circuito da Figura P12.28 são R = 2,5 kV; L = 50 mH e C = 2 nF. Se Icc = 40 mA, determine i o(t) para t $ 0.
Aplique os teoremas do valor inicial e do valor final a cada par de transformadas do Problema 12.40.