Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 6

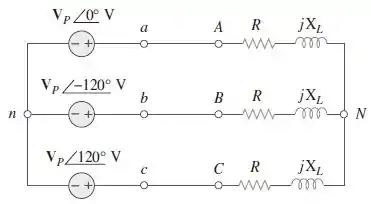
Considere a Figura e elabore um problema para ajudar outros estudantes a entender melhor a conexão estrela-estrela equilibrada.

Passo 1

Vamos resolver o seguinte problema “para o circuito com conexão estrela-estrela, encontre as correntes de linha e tensão de linha dado que e ”.

Numa conexão estrela, a tensão de linha e a tensão de fase se relacionam da seguinte maneira:

Substituindo os valores, temos:

Passo 2

Uma vez que temos a tensões de linha e de fase, para encontrarmos a corrente de linha é tranquilo. Na conexão estrela, a corrente de linha é igual a corrente de fase! Logo, para calcularmos a corrente de linha, basta dividirmos a tensão de fase pela impedância de fase.

Logo,

As correntes, então, serão iguais a:

Resposta

As tensões de linha são iguais a:

As correntes de linha são iguais a:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a potência entregue à carga do Ex. 13.5.1 for medida pelos dois wattímetros A e C ligados como mostrado na Fig. 13.20, calcule a leitura dos wattímetros. Verifique a consistência com a resposta do

Calcule as leituras dos wattímetros P A e P C e a potência total P da Fig. 13.20 se as tensoes de Iinha forem como dado no Ex. 13.5.1 e Z 1 = Z 2 = Z 3 = 10 ∠ 75 ° . Confirme a resposta usando P = 3 P

14-Um circuito trifásico equilibrado é caracterizado da seguinte forma: • Está ligado em Y-D; • A tensão da fase b da fonte b é 150l135° V; • A sequência de fases da fonte é acb; • A impedância de lin

13-Uma carga equilibrada, ligada em D, tem uma impedância de 216 + j288 V/f. A carga é alimentada por uma linha cuja impedância é 3 + j5 V/f. A tensão de fase nos terminais da carga é 7,2 kV. A sequên

10-Um circuito trifásico equilibrado tem as seguintes características: • Está ligado em Y-Y; • A tensão de linha na fonte, Vab, é 110!3 l -60° V; • A sequência de fases é positiva; • A impedância de l