Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 7
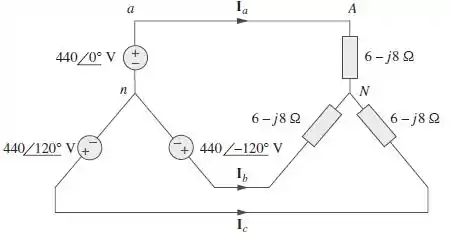
Obtenha as correntes de linha no circuito trifásico da Figura .
Passo 1
Galera, estamos diante de um sistema trifásico, equilibrado e com conexão estrela-estrela. Portanto, encontrar a corrente de linha é tranquilo, uma vez que as correntes de linha são iguais as correntes de fase:
Para isso, precisamos passar a impedância de fase para a forma polar:
Portanto, as correntes de linha são iguais a:
Resposta
As correntes de linha são iguais a:
Exercícios de Livros Relacionados
Calcule as leituras P A e P B dos wattímetros e a potência total entregue à carga se a fonte é equilibrada, conectada em Y , sequência a b c , com V a n = 100 ∠ 0 ° V (eficazes), e as impedâncias de f
Repita o Prob. 13.31, se Z 1 = Z 2 = Z 3 = 10 ∠ 60 °Ω . Note que, neste caso, o wattímetro C lê a potência total, pois o wattímetro A lê zero.
Mostre, que na Fig. 13.20, se V a b = V L ∠ α V, V b c = V L ∠ ( α - 120 ° ) V e V c a = V L ∠ ( α - 24 0 ° ) V (eficazes), e Z 1 = Z 2 = Z 3 = Z ∠ 60 °Ω , então o wattímetro A lê zero e o wattímetro
No Prob. 13.36, calcule o fator de potência da carga, se (a) P A = P C , (b) P A = - P C , (c) P A = 0 , (d) P C = 0 e (e) P A = 2 P C .
Para o sistema mostrado abaixo, as tensões de linha são um conjunto equilibrado de sequência positiva com V a b = 300 ∠ 0 °V (eficazes). Calcule a leitura dos medidores P A e P B e a potência total en