Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 26
Considere a Figura 12.55 e elabore um problema para ajudar outros estudantes a entender melhor fontes em delta equilibradas que alimentam cargas em estrela equilibradas.
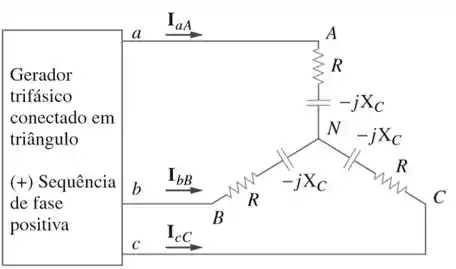
Passo 1
E o jogo virou novamente! Vamos lá! O problema vai ser assim: Para o circuito balanceado na Fig. 12.55, V. Encontre as correntes de linha .
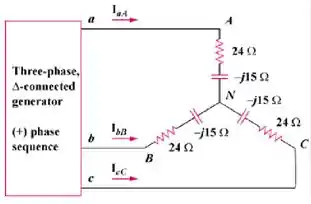
Passo 2
Questão bem de boas! Primeiro transformamos a fonte para um equivalente em estrela!
Agora usamos um equivalente por fase!
Resposta
Exercícios de Livros Relacionados
Na Fig. 13.13, a fonte é equilibrada, com sequência de fases positiva, e V a n = 100 ∠ 0 ∘ V (eficazes). Se a impedância de fase é 3 3 ∠ 30 ∘ Ω , calcule a corrente de linha e a potência entregue à ca
Na Fig. 13.13, o sistema de sequência positiva tem V a n = 200 ∠ 0 ∘ V ( eficazes). Calcule Z p , se a fonte entrega 2,4k W , com fator de potência 0,8 atrasado
Uma fonte equilibrada conectada em Y , c o m V a n = 2400 V (eficazes), de seqüência positiva, é conectada por quatro condutores perfeitos a uma carga desbalanceada conectada e m Y , Z A N = 10 Ω ,
Repita o Prob. 13.31 , se Z 1 = Z 2 = Z 3 = 10600 ∘ Ω . Note que, neste caso, o wattímetro C lê a potência total, pois o wattímetro A lê zero.
No sistema Y = Δ equilibrado, a carga consome 3k W , com fator de potência 0,8 atrasado. Capacitores sáo conectados a cada fase da carga, para aumentar seu fator de potência para 0,9 atrasado. Calcule