Considere a Figura abaixo e elabore um problema para ajudar outros estudantes a entender melhor a energia em circuitos acoplados.
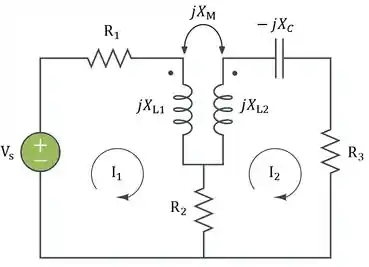
Passo 1
Vamos trabalhar com o seguinte problema: encontrar e do circuito da figura abaixo e posteriormente calcular a potência absorvida pelo resistor de .
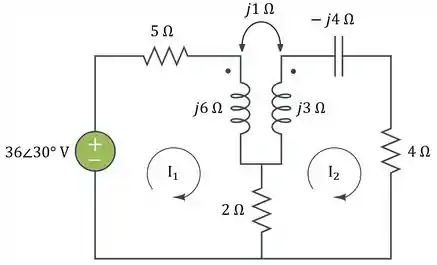
Passo 2
Primeiramente vamos substituir o circuito acoplado mutuamente pela fonte dependente equivalente. Primeiro determinaremos as tensões induzidas e, em seguida, definimos os sinais adequados. Sabemos que:
A corrente induz uma tensão na segunda bobina representada pelo valor , e induz uma tensão de na primeira bobina. Portanto, a tensão induzida na segunda bobina é e na primeira bobina é .
Para descobrir a polaridade da tensão mútua na bobina 1 devido à corrente , observamos que sai pela extremidade do ponto de induzindo uma tensão em com um sinal + no lado inferior e um sinal – no lado superior. A corrente entra em pelo lado do ponto e induz uma tensão em com um sinal + no lado superior e um sinal – no lado inferior.
Então o circuito equivalente com as fonte dependentes é mostrado a seguir:
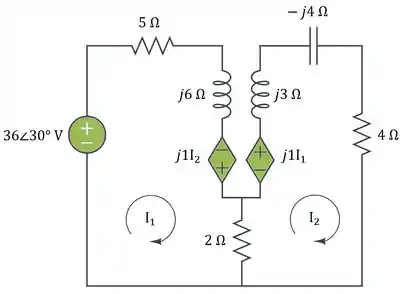
Passo 3
Para a malha 1 da Figura anterior, a LKT fornece:
Para a malha 2, temos:
Colocando as equações das malhas na forma matricial, obtemos:
Passo 4
Os determinantes são:
Portanto, obtemos as correntes de malha como segue:
Passo 5
A potência absorvida pelo resistor de
Resposta
Portanto, as correntes e são:
E a potência absorvida pelo resistor de é :