Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 27

Determine a potência média liberada para o resistor de 50   Ω no circuito da Figura 13.96 .

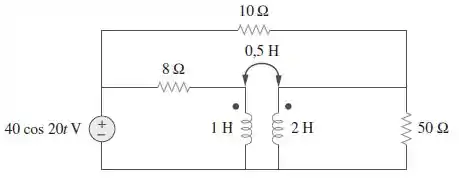
Passo 1

Pessoal, vamos passar os elementos do circuito do domíno do tmepo para o domnídio da frequência:

40 cos ⁡ 20 t   V   →     40 ∠ 0 °   V

L 1 = 1   H   →     X L 1 = j ω L 1 = j 20   Ω

L 2 = 2   H   →     X L 2 = j ω L 2 = j 40   Ω

M = 0,5   H   →     X M = j ω M = j 10   Ω

Passo 2

Vamos nos concentrar no circuito abaixo para realiar nossa análise:

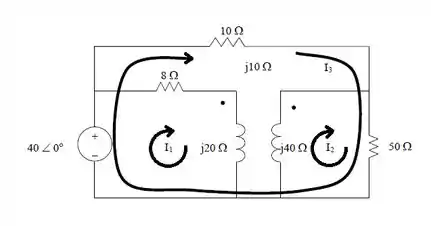
Vamos aplicar a lei das malhas no nosso circuito. Para a malha 1 ,

- 40 + 8 I 1 + j 20 I 1 - j 10 I 2 = 0

8 + j 20 I 1 - j 10 I 2 = 40 … 1

Para a malha 2 ,

j 40 I 2 - j 10 I 1 + 50 I 2 + I 3 = 0

- j 10 I 1 + 50 + j 40 I 2 + 50 I 3 = 0 … ( 2 )

Para a malha 3 ,

- 40 + 10 I 3 + 50 I 3 + I 2 = 0

50 I 2 + 60 I 3 = 40 … ( 3 )

Passo 3

Vamos escrever na forma matricial?

8 + j 20 - j 10 0 - j 10 50 + j 40 50 0 50 60 I 1 I 2 I 3 = 40 0 40   →     A X = [ b ]

Para encontrarmos os valores e I 1 , I 2 e I 3 podemos usar a regra de Cramer! Primeiro de tudo, vamos calcular o determinante da matriz A :

det ⁡ A = 8 + j 20 - j 10 0 - j 10 50 + j 40 50 0 50 60

det ⁡ A = - 38000 + j 29200

Agora, vamos substituir a matriz [ b ] em cada uma das colunas para calcular os determinantes, a fim de encontrarmos os valores de cada uma das variáveis. Para I 1 :

det ⁡ A I 1 = 40 - j 10 0 0 50 + j 40 50 40 50 60

det ⁡ A I 1 = 20000 + j 760 00

Para I 2 :

det ⁡ A I 2 = 8 + j 20 40 0 - j 10 0 50 0 40 60

det ⁡ A I 2 = - 16000 - j 16 000

Para I 3 :

det ⁡ A I 3 = 8 + j 20 - j 10 40 - j 10 50 + j 40 0 0 50 40

det ⁡ A I 3 = - 1 2 0 00 + j 32800

Passo 4

Para encontrarmos os valores das correntes é simples!

I 1 = det ⁡ A I 1 det ⁡ A = 20000 + j 76000 - 38000 + j 29200 = 0,63 - j 1,51   A

I 2 = det ⁡ A I 2 det ⁡ A = - 16000 - j 16000 - 38000 + j 29200 = 0,06 + j 0,468   A

I 3 = det ⁡ A I 3 d e t ⁡ ( A ) = - 12000 + j 32800 - 38000 + j 29200 = 0,615 - j 0,39   A

A corrente que passar pelo resistor de 50   Ω é igual a:

I 50 = I 2 + I 3

I 50 = 0,0613 + 0,6156 + j 0,4682 - 0,3901

I 50 = 0,6769 + j 0,0781

I 50 = 0,6814 ∠ 6,58 °   A

O valor R M S da corrente é igual a:

I 50 r m s = 0,6814 2 = 481,8   m A

Assim, a potência média liberada para o resistor de 50   Ω é:

P = I 50 r m s 2 R

P = 0,4818 2 50 = 11,608   W

Resposta

A potência é igual a:

P = 11,608   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a corrente I 0 no circuito da Figura 13.91 .
Refaça o problema 13.22 usando o PSpice ou MultiSim.
Use o PSpice ou MultiSim para determinar as corretes de malha no ircuito da Figura 13.140 . Adote ω = 1r a d / s . Na resolução esse problema use k = 0,5 .
Use o PSpice ou MultiSim para encontrar I 1 , I 2 e I 3 no circuito da Figura 13.141 .