Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 70
Considere a figura e elabore um problema para ajudar outros estudantes a entender melhor como fazer a análise de circuito no domínio s em circuitos que têm elementos mutuamente acoplados.
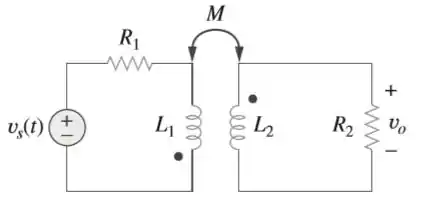
Passo 1
Vamos criar um problema com valores reais:
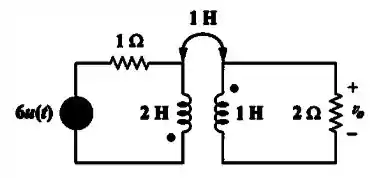
Passo 2
Agora, vamos passar esse circuito para o domínio de Laplace (domínio s):
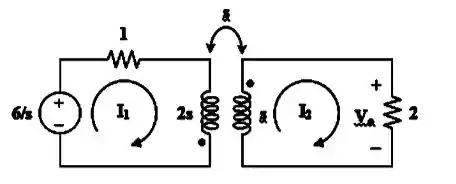
Passo 3
Agora podemos aplicar a lei de Kirchhoff das tensões na malha 1 e teremos a equação 1:
Depois, faremos a lei de Kirchhoff das tensões na malha 2 e teremos a equação 2:
Substituindo então a equação 2 na equação 1, vamos encontrar :
Passo 4
Daí, podemos usar essa corrente para encontrar
Passo 5
Separando em frações parciais teremos:
Agora basta encontrar e encontrar .
Daí, substituindo, teremos:
Por Laplace utilizando a tabela de transformadas, teremos:
Resposta
Exercícios de Livros Relacionados
As duas chaves no circuito da Figura P13.35 funcionam simultaneamente. Não há nenhuma energia armazenada no circuito no instante em que elas se fecham. Determine i(t), para t ≥ 0+, a partir do equival
A chave no circuito da Figura P13.28 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente para a posição b. a) Determine Vo. b) Determine vo.
Começando com a Equação 13.65, mostre que a corrente no capacitor do circuito da Figura 13.19 é positiva para 0 μs e negativa para t200 μ s. Mostre também que em 200 μ s a corrente é nula e que isso c