Determine e no circuito da figura:

Passo 1
Desenhando o circuito no domínio de Laplace:
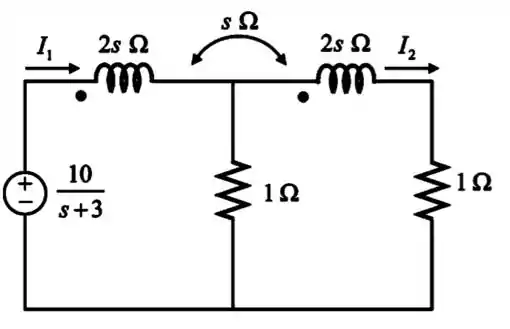
Passo 2
Agora podemos aplicar a lei de Kirchhoff das tensões na malha 2 e isolar o nosso
Depois, faremos a lei de Kirchhoff das tensões na malha 1 e isolaremos o nosso
Passo 3
Em seguida, a gente substitui o valor de que encontramos e substituímos na expressão de , encontrando assim, as respostas!
Note que, como ele não pede as correntes em função do tempo, então não precisamos usar nada de Laplace!