Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 71

Considere o circuito com transformador ideal da figura, determine i o ( t ) .

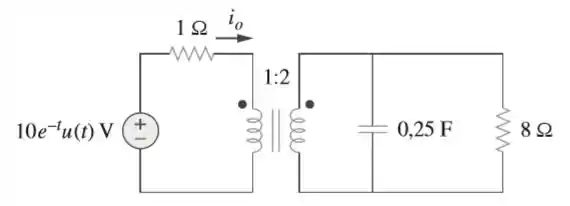
Passo 1

Primeiro vamos achar a impedância equivalente do paralelo:

Z L = 8 / / 4 s = 8 2 s + 1

Passo 2

Em seguida, refletimos essa impedância para o lado primário sabendo que n = 2 :

Z i n = 1 + Z L n 2 → 2 s + 3 2 s + 1

E para calcular a corrente I o :

I o = 10 s + 1 × 1 Z i n = 10 s + 1 × 2 s + 1 2 s + 3

Passo 3

Separando em frações parciais teremos:

I o = 10 s + 5 ( s + 1 ) ( s + 1.5 ) = A s + 1 + B s + 1.5

Agora basta encontrar A   e   B   :

A =   - 10

B = 20

Daí, substituímos e por Laplace utilizando a tabela de transformadas, teremos:

i ( t ) = 10 [ 2 e - 1.5 t - e - t ] u ( t )   A

Resposta

i ( t ) = 10 [ 2 e - 1.5 t - e - t ] u ( t )   A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A chave no circuito da Figura P13.13 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente de a para b. a) Construa um circuito no domínio da frequência, para t0. b) Determine V
a) Determine a expressão de V o no domínio da frequência, para o circuito da Figura P13.17. b) Use a expressão no domínio da frequência determinada em (a) para prever os valores inicial e final de v o
A chave no circuito da Figura P13.12 esteve fechada por um longo tempo. Em t = 0, ela é aberta. a) Determine i o, para t $ 0. b) Determine vo, para t $ 0. b) Determine vo, para t $ 0.
Não há nenhuma energia armazenada no circuito da Figura P13.22, em t = 0-. a) Determine Vo. b) Determine vo. c) A solução para vo faz sentido em termos do comportamento conhecido do circuito? Explique
Não há nenhuma energia armazenada no circuito da Figura P13.19, em t = 0 - . a) Use o método das tensões de nó para determinar i 0 . b) Determine a expressão no domínio do tempo para v 0 . c) Suas res