Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 77
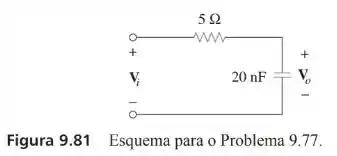
Consulte o circuito da figura 9.81.
Calcule o deslocamento de fase em .
Determine a frequência em que o deslocamento de fase é .
Passo 1
Vamos ter que o deslocamento em fase vai ser dado por
Onde essas duas grandezas se relacionam através da seguinte equação
Aqui devemos destacar quem é que é dado nada mais nada menos que por
Passo 2
Com as informações dadas acima vamos ter que
Sendo assim, vamos ter
Passando para forma trigonométrica vamos ter
Um atraso de .
Passo 3
Por fim, para acharmos a frequência desejada vamos utilizar a seguinte fórmula
Dado que vamos ter
Dessa equação podemos concluir que visto que o arco cuja tangente vale é o arco de . Assim, temos que
Resposta
Exercícios de Livros Relacionados
Considere o circuito comutador de fase da figura 9.83. Seja V i = 120 V , operando a 60 H z . Determine: a V 0 quando R é máxima. b V 0 quando R é mínima. c O valor de R que produzirá um deslocamento
a Calcule o deslocamento de fase do circuito da Figura 9.82. b Informe se o deslocamento de fase está avançado ou atrasado (saída em relação à entrada). c Determine a magnitude da saída quando a entra
Uma ponte de capacitância está equilibrada quando R 1 = 1 00Ω ,R 2 = 2 k ΩeC s = 40μ F . Qual o valor de C x , a capacitância do capacitor em teste?
Uma ponte indutiva fica em equilíbrio quando R 1 = 1,2k Ω ,R 2 = 500 ΩeL s = 250m H . Qual o valor de L x , a indutância do indutor em teste?