Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 9.Problemas - Ex. 64

64- Determine Z_T e I no circuito da Figura 9.71

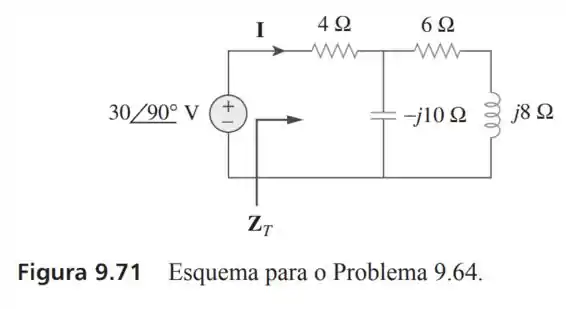
Passo 1

Caso não tenha dada para entender Z_T é a impedância do circuito todo. E ela pode ser calculada fazendo:

Z_T = 4 + (1)/((1)/(- j 10) + (1)/(6 + j 8))

Isso é,fazendo a impedância paralela entre - j 10 e 6 + j 8 em série com a resistência de 4 omega . Logo:

Z_T = 4 + (- j 60 + 80)/(- j 2 + 6)

Z_T = (- j 8 + 24 - j 60 + 80)/(- j 2 + 6)

Z_T = (10 4 - j 68)/(6 - j 2) = (12 4.2578 /_ - 3 3.1785)/(6.324555 /_ - 18.435)

Z_T = (19 . 647 /_ - 14 . 7435) omega = (19 - j 5) omega

Passo 2

Dessa forma a corrente total I será, a razão entre a tensão e a impedância:

V = Z I

I = (V)/(Z) = (30 /_ 90)/(19.647 /_ - 14.7435) = 1.5 27 /_ 104 . 744 ° A

Resposta

Z_T = (19.647 /_ - 14.7435) omega = (19 - j 5) omega

I = 1.527 /_ 104.744 ° A

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que se R eZ = R e positivo, logo R e Y = R e 1 Z = G e tambem positivo.
Um circuito tem uma impedância. z = 16 ( 2 + j w ) ( 8 - w 2 - j 2 w ) w 4 - 15 w 2 + 64Ω Calcule a resistência e a reatância com w = 1,2e3 r a d s . Se a tensão no domínio do tempo aplicada ao circui
Mostre que a frequência de ressonância. no caso da função do Ex. 15.2.1, coincide com a frequência para a qual a função e real.
No Ex. 15.3.2(a), calcule a amplitude para a tensão na associação se a fonte de corrente é i g = cos ⁡ ω t mA e ω é (a) 10 4 , (b) 5 · 10 4 e (c) 25 · 1 0 4r a d / s .
Faça a resposta em amplitude | H ( j ω ) | ser tal que H j ω M a x = H j 0 = K , de forma que no corte H j ω c = K / 2 . Calcule a perda, dada por (15.38), em ω = 0 e em ω = ω c . Note que ω c corresp