Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 1.Problemas - Ex. 8
A corrente que flui por um ponto em um dispositivo é mostrada na figura . Calcule a carga total através do ponto.
Passo 1
Vamos lá, o que a gente tem aqui é um gráfico de corrente por tempo.
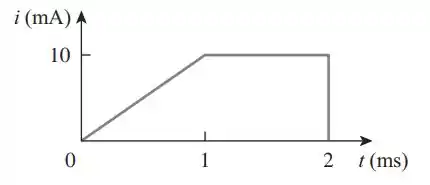
Lembra do seguinte: a carga que passa por um fio é a integral da corrente no tempo. Então é só a gente achar a área que está abaixo desse gráfico, porque isso que é a integral!
Passo 2
A área desse gráfico é a área do trapézio. Ele tem uma base igual a , a outra base igual a e a altura de . Sua área vai ser:
Resposta
Exercícios de Livros Relacionados
Determine a corrente que flui por um elemento se o fluxo de carga for dado por: q t = 3 t + 8m C q t = 8 t 2 + 4 t - 2C q t = 3 e - t - 5 e - 2 tn C q t = 10s e n 120π tp C q t = 20 e - 4 t cos ( 50
Quantos coulombs são representados pelas seguintes quantidades de elétrons? 6,482 × 10 17 1,24 × 10 18 2,46 × 10 19 1,628 × 10 20
1.7 A carga que flui por um fio é representada na Figura 1.24. Represente a corrente correspondente.
A corrente através de um elemento é ilustrada na figura 1.26 . Determine a carga total que passa pelo elemento em: t = 1s t = 3s t = 5s