Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 38
38. Um transformador de , , foi projetado para ter uma induzida de . Supondo o transformador ideal, calcule:
a) O número de espiras do enrolamento de alta tensão , .
b) O número de espiras do enrolamento de baixa tensão , .
c) A corrente nominal para o enrolamento de , .
d) A corrente nominal para o enrolamento de , .
e) A relação de transformação.
Passo 1
Com os dados que o enunciado nos fornece, vamos desenhar o esquema desse transformador.
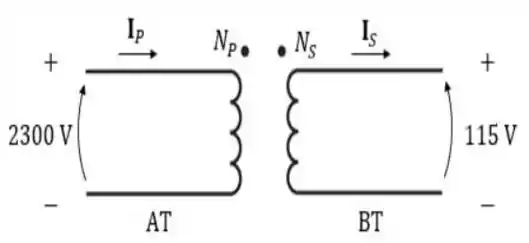
Passo 2
Na letra (a), precisamos encontrar o número de espiras do primário. O enunciado nos disse que a induzida é de , ou seja, que para cada espira temos . Logo, para encontrar o número de espiras vamos usar a equação abaixo.
Passo 3
Fazendo o mesmo para o lado de baixa tensão na letra (b), temos que...
Passo 4
Na letra (c), precisamos encontrar a corrente no primário. O enunciado nos disse que o transformador é de , ou seja,
Como...
Passo 5
Agora, vamos usar a relação de transformação do transformador para encontrarmos a corrente no lado de baixa tensão na letra (d).
Passo 6
Para terminar, na letra (e), temos que calcular a relação de transformação...
E voilà! Respostas encontradas com sucesso!