Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 40

40. O primário de um transformador ideal com relação de espiras igual a 5 é conectado a uma fonte de tensão com parâmetros de T h é v e n i n V T h = 10   c o s   2.000 t   V   e R T h = 100   Ω . Determine a potência média liberada para uma carga de 200   Ω   no enrolamento secundário.

Passo 1

Olha só! O nosso circuito está disposto desse jeito...

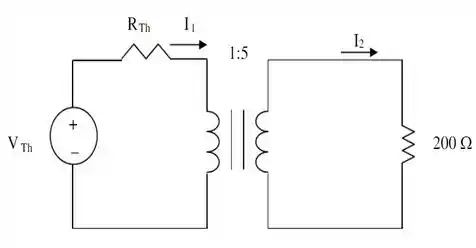
E a primeira coisa, a se fazer; como temos uma fonte de tensão senoidal, é passa-la para o domínio da frequência...

10   c o s   2.000 t → 10 ∠ 0 °     ,   ω = 2000   r a d / s  

Feito isso! Vamos correr agora, atrás de determinar a corrente I 1 . Para isso, bora tratar de refletir o resistor de 200   Ω para o primário.

R 2 ' = α 2 R 2

Logo, temos que usar a relação de transformação abaixo

α = N 1 N 2

Onde olhando a figura anterior, vemos que:

α = N 1 N 2 = 1 5

α = 0,2

Passo 2

Refletindo a resistência de 200   Ω , temos que:

R 2 ' = ( 0,2 ) 2 ⋅ ( 200   Ω )

R 2 ' = 8   Ω

Portanto, o circuito equivalente série do transformador referido ao primário será...

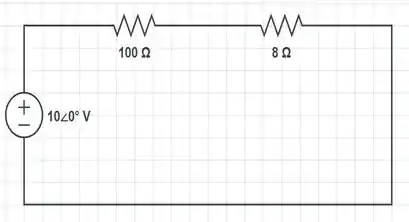
Desse modo, aplicando a Lei de O h m :

I 1 = 10 ∠ 0 ° 100 + 8

I 1 = 92,59 ∠ 0 °   m A

Passo 3

E em seguida, vamos calcular I 2 . Pela relação de transformação, temos:

α = N 1 N 2 = I 2 I 1

Logo...

I 2 I 1 = α

I 2 = α I 1

I 2 = ( 0,2 ) ( 92,6 ∠ 0 °   m A )

I 2 = 18,52 ∠ 0 °   m A

Obtida essa corrente, falta apenas determinar a potência média liberada para a carga de 200   Ω   no secundário. Pois bem! Ela é dada pela fórmula abaixo:

P = 1 2 | I 2 | 2 R L

P = 1 2 0,01852   A 2 ( 200   Ω )

P = 0,03429   W

P ≅ 34,3   m W

Resposta

P ≅ 34,3   m W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a potência média por cada resistor no circuito da Figura 13.123 .
Elabore um problema para ajudar outros estudantes a entender melhor como funciona o transformador ideal.
Um autotransformador com uma derivação de 40 % é alimentado por uma fonte de 400V ,60H z e é usado para operação de redução de tensão. Uma carga é 5 k V A operando com fator de potência unitário é con
No circuito com autotransformador da Figura 13.134 , demonstre que Z e n t = 1 + N 1 N 2 2 Z L
No circuito da Figura 13.132 , Z L é ajustada até a máxima potência media ser liberada para Z L . Determinar Z L e a máxima potência média transferida para ela. Considere N 1 = 600 espiras e N 2 = 200