Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 11.Problemas - Ex. 2
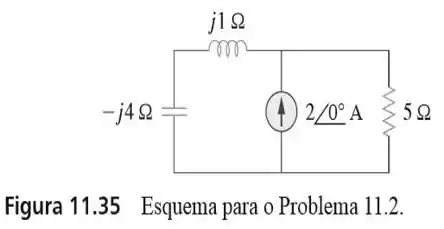
2. Dado o circuito da Figura , determine a potência média fornecida ou absorvida por cada elemento.
Passo 1
Olha só! Nós aprendemos na teoria, que apenas cargas resistivas absorvem potência. Capacitores e indutores não absorvem potência. Então, a potência absorvida no resistor será igual a potência fornecida pela fonte.
Passo 2
Desse modo, vamos calcular a potência absorvida pelo resistor através da fórmula abaixo:
Para isso, precisamos encontrar a corrente que passa pelo resistor. Então, aplicando divisor de corrente no circuito abaixo, temos que:
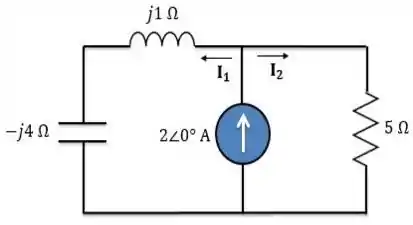
Passando para a forma polar:
Essa é a corrente procurada!
Passo 3
E aplicando a fórmula, em seguida:
Portanto, a potência absorvida pelo resistor e fornecida pela fonte de corrente é . Além disso, o capacitor e o indutor não absorvem potência.
Resposta
A potência absorvida pelo resistor e fornecida pela fonte de corrente é . Além disso, o capacitor e o indutor não absorvem potência.