Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 12.Problemas - Ex. 12
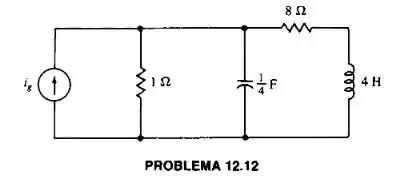
Calcule a potência média entregue ao resistor de se .
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Primeiramente, vamos resolver por superposição, já que é uma fonte de corrente que tem diferentes frequências, na primeira parte da superposição, vamos pegar a fonte constante, no caso
Consequentemente, não tem frequência, logo, indutores e capacitores são tirados da jogada, com isso, temos o seguinte circuito
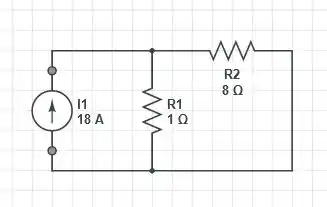
Com isso, a tensão será igual a
E a corrente
Agora, vamos analisar a segunda parcela da fonte de corrente
Passo 2
Vamos analisar a parcela , com isso, o circuito exatamente da seguinte forma
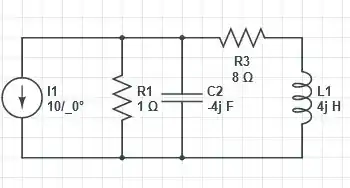
A impedância equivalente nesse caso é igual a
A corrente pelo resistor de , nós vamos chamar , no caso, ela vai ser igual a
Com isso, o valor RMS será igual a
Passo 3
Analisando a terceira parcela, o macete aqui é somente os parâmetros nos componentes já que o circuito não muda a sua característica, com isso, nós temos que
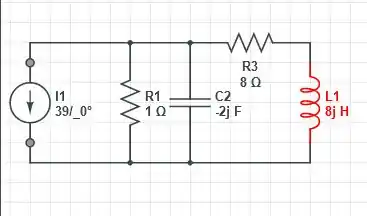
Com isso, a impedância será calculada seguindo a mesma lógica da segunda parcela, com isso, nós obtemos o seguinte resultado
Com isso, a corrente que passa pelo resistor de é igual a
Logo, o valor RMS é igual a
Passo 4
Por fim, a última parcela, , agora vamos ter a seguinte configuração de circuito
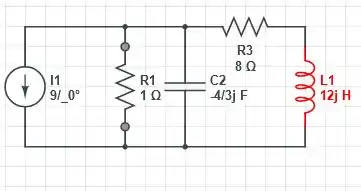
A impedância equivalente será igual a
Com isso, a corrente que passa pelo resistor de é igual a
Logo, o valor RMS é igual a
Passo 5
E finalmente, vamos calcular a potência, somando os valores das correntes encontradas, portanto, a potência no resistor é igual a
O termo é basicamente
Substituindo os valores, nós temos que
Desenvolvendo um pouco mais
Com isso, a potência no resistor é igual a