Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 13.Problemas - Ex. 28

Demonstre (13.24).

Passo 1

Falaeee feraaa!! Beleza? A gente sempre aprendeu a formulazinha de como passar um circuito delta para um circuito estrela e vice versa. Mas vc sabe como chegar nelas? Vem comigo aquiii!!!

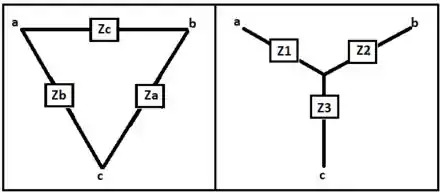
Para fazermos a transformação Delta -> Y , vamos observar as seguintes impedâncias organizadas em Delta e em Y , respectivamente:

Passo 2

Imagine agora que coloquemos um multímetro nos terminais a e b do circuito Delta para descobrirmos a impedância equivalente. Assim, temos que:

Z_a b = (Z a + Z b) | | Z c

Da mesma forma, para as outras impedâncias, temos:

Z_b c = (Z b + Z c) | | Z a

Z_a c = (Z a + Z c) | | Z b

Passo 3

Agora vamos fazer a mesma coisa no circuito Y a fim de verificar as impedâncias equivalentes entre os terminais a e b :

Z_a b = Z 1 + Z 2

Fazendo o mesmo para os outros terminais, temos:

Z_b c = Z 2 + Z 3

Z_a c = Z 1 + Z 3

Passo 4

Igualando as impedâncias equivalentes que acabamos de descobrir de Delta e Y , temos:

Z_a b_Delta = Z_a b_Y :.

((Z a + Z b) xx Z c)/((Z a + Z b) + Z c) = Z 1 + Z 2

Z_b c_Delta = Z_b c_Y :.

((Z b + Z c) xx Z a)/((Z b + Z c) + Z a) = Z 2 + Z 3

Z_a c_Delta = Z_a c_Y :.

((Z a + Z c) xx Z b)/((Z a + Z c) + Z b) = Z 1 + Z 3

Para ficar mais simples de entender, vamos fazer o seguinte:

k 1 = ((Z a + Z b) xx Z c)/((Z a + Z b) + Z c)

k 2 = ((Z b + Z c) xx Z a)/((Z b + Z c) + Z a)

k 3 = ((Z a + Z c) xx Z b)/((Z a + Z c) + Z b)

Portanto, temos:

k 1 = Z 1 + Z 2 :. Z 1 = k 1 - Z 2

k 2 = Z 2 + Z 3 :. Z 2 = k 2 - Z 3

k 3 = Z 1 + Z 3 :. Z 3 = k 3 - Z 1

Passo 5

Agora, substituindo Z 3 em Z 2 , temos:

Z 2 = k 2 - k 3 + Z 1

E, substituindo esse valor de Z 2 em Z 1 , temos:

Z 1 = k 1 - k 2 + k 3 - Z 1 :. Z 1 = (k 1 - k 2 + k 3)/(2)

Passo 6

Agora vamos substituir os valores de k 1 , k 2 e k 3 que a gente descobriu antes nessa última equação de Z 1 :

Z 1 = ([(Z a + Z b) xx Z c] - [(Z b + Z c) xx Z a] + [(Z a + Z c) xx Z b])/(2 ( Z a + Z b + Z c ))

Desenvolvendo Z 1 , temos:

Z 1 = (Z a Z c + Z b Z c - Z a Z b - Z a Z c + Z a Z b + Z b Z c)/(2 (Z a + Z b + Z c)) :.

Z 1 = (2 Z b Z c)/(2 (Z a + Z b + Z c)) :.

Z 1 = (Z b Z c)/((Z a + Z b + Z c))

Passo 7

Fazendo a mesma coisa para Z 2 e Z 3 , teremos que:

Z 2 = (Z a Z c)/((Z a + Z b + Z c))

Z 3 = (Z a Z b)/((Z a + Z b + Z c))

É bem simples, porém fácil de se confundir. Mas aqui a gente consegue tudo B)

Resposta

Z 1 = (Z b Z c)/((Z a + Z b + Z c))

Z 2 = (Z a Z c)/((Z a + Z b + Z c))

Z 3 = (Z a Z b)/((Z a + Z b + Z c))

Exercícios de Livros Relacionados

Encontre as leituras dos wattímetros, conectados como no Prob. 13.34, para o sistema do Prob 13.23.
Repita o Prob. 13.38 para o sistema do Prob. 13.27.
Repita o Prob. 13.4 . 1 para o sistema do Prob.
Na Fig. 13.18, com Z 1 = Z 2 = Z 3 = 20 ∠ 30 ° Ω , e considerando as tensoes de Iinha como um conjunto equilibrado de sequência abc, com V a b = 100 ∠ 0 °V (eficazes). CaIcule a leitura de cada medido
Se a potência entregue à carga do Ex. 13.5.1 for medida pelos dois wattímetros A e C ligados como mostrado na Fig. 13.20, calcule a leitura dos wattímetros. Verifique a consistência com a resposta do