Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 13.Problemas - Ex. 24

Uma fonte trifásica equilibrada, de sequência positiva, com V a b = 2 0 0 ∠ 0 °   V (eficazes), está alimentando uma carga conectada em Δ , Z A B = 50   Ω , Z B C = 20 + j 20   Ω e Z C A = 30 - j 40   Ω . Calcule as correntes de linha.

Passo 1

Eaeee, se liga que essa é muuuuito parecida com a questão passada!!

Seguinte, a gente tem esse circuitinho aqui:

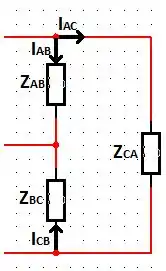
Considerando a sequência positiva da fonte trifásica, temos as seguintes correntes de fase:

I A B = V A B Z A B ∴ I A B = 2 0 0 ∠ 0 ° 50 = 4 ∠ 0 °   A  

I B C = V B C Z B C ∴ I B C = 2 0 0 ∠ - 120 ° 20 + j 20 = 5 2 ∠ - 165 °   A

I C A = V C A Z C A ∴ I C A = 2 0 0 ∠ 120 ° 30 - j 40 = 4 ∠ 173.13 °   A

Passo 2

Pela Lei dos nós, podemos obter as correntes de linha. Se liga:

I A = I A B - I A C ∴ I A = 4 ∠ 0 °   A   - 4 ∠ 173.13 ° ≈ 8 ∠ - 3.4 °   A

I B = - ( I A B + I C B ) ∴ I A = - 4 - 5 2 ∠ - 165 ° ≈ 11 ∠ - 170 . 4 °   A

I C = I C B - I A C ∴ I C = 4 ∠ 173.13 ° - 5 2 ∠ - 165 ° ≈ 3.67 ∠ 3 8.92 °   A

E aí... belezinha? Bora pra próxima!!

Resposta

I A = 8 ∠ - 3.4 °   A

I B = 11 ∠ - 170.4 °   A

I C = 3.67 ∠ 38.92 °   A

Exercícios de Livros Relacionados

Uma fonte trifásica equilibrada, de sequência positiva, com V a b = 200 ∠ 0 °V (eficazes), está alimentando uma carga conectada em Δ , Z A B = 20Ω , Z B C = 20 ∠ 60 °Ω e Z C A = 50 ∠ 30 °Ω . Calcule o
No sistema Y - Δ do Prob. 13.17, a tensão da fonte, V a n = 100 ∠ 0 °V (eficazes) e Z P = 10 ∠ 60 °Ω . Calcule a tensão de linha, a corrente de linha, os módulos da corrente da carga e a potência entr
Para o sistema Y - Δ do Prob. 13.17, Z p = 4 - j 3Ω e a potência entregue à carga é 19.2k W . Calcule a corrente de linha I L e as tensões de fase da fonte, se V a n for tomada como referência.
No sistema Y - Δ mostrado na figura, a fonte é de sequência positiva com V a n = 100 ∠ 0 ° V (eficazes) e a impedância de fase é Z p = 3 - j 4Ω . Calcule a tensão de linha V L , a corrente de linha I