Desenvolva as equações de estado para o Problema .
Passo 1
O circuito em questão é o seguinte:
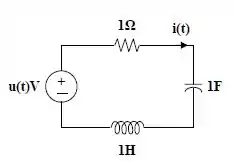
Vamos chamar a tensão do capacitor de e a tensão no indutor igual a . Aplicando a lei das malhas no circuito, temos:
Passo 2
A corrente que circula pelo capacitor pode ser escrita como:
Escrevendo as equações de estado, temos:
Resposta
As equações de estado são: