Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 42

(a) Se a chave na Figura 7.109 tiver sido aberta há um bom tempo e for fechada em t   =   0 , determine v o ( t ) .

(b) Suponha que a chave se encontre fechada há um longo período e seja aberta em   t   =   0 . Determine v o ( t ) .

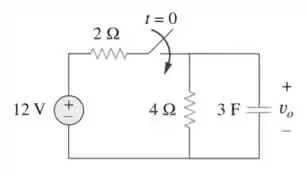
Passo 1

Questão bem tranquila galera, nada desafiador para a gente! Vamos que vamos! Primeiro vamos aplicar a fórmula vindo da EDO. Para o item a ) , temos que:

v 0 t = v 0 ∞ + v 0 0 - v 0 ∞ e - t / τ

v 0 = 0   V ,   v ∞ = 4 4 + 2 12 = 8   V

τ = R e q C e q ,   R e q = 2 | | 4 = 4 3   Ω

τ = 4 3 3 = 4

Portanto,

v 0 t = 8 - 8 e - t / 4   V

Passo 2

Passando para o item b ) temos uma coisa bem interessante! v 0 ∞ = 0 . Sim, você não entendeu errado! Isso acontece porque o capacitor “fica de fora” da malha. Logo,

v 0 t = v 0 0 e - t / τ

Bem tranquilo, logo temos que:

v 0 0 = 4 4 + 2 12 = 8   V

τ = R C = 4 ⋅ 3 = 12

Portanto,

v 0 t = 8 e - t / 12   V

Resposta

a ) v 0 t = 8 - 8 e - t / 4   V

b ) v 0 t = 8 e - t / 12   V  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine v 0 no circuito da Figura 7.112 quando v s=30 u ( t )V . Suponha que v 0 ( 0 )=5V .
Usando a Figura 7.108, elabore um problema para ajudar outros estudantes a entenderem melhor a resposta de um circuito RC.
A chave na Figura 7.111 se encontra na posição a há um bom tempo. Em t=0 , ela é mudada para a posição b . Calcule i ( t ) para todo t0 .
Determine a tensão no capacitor para t0 e t0 para cada um dos circuitos da Figura 7.107
Considere o circuito da Figura 7.110. Determine i ( t ) para t 0 e t0 .