Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 84
Um circuito em paralelo possui e . A entrada para o circuito é . Determine a corrente no indutor para todo e suponha que .
Passo 1
Antes de desenhar o circuito, vamos calcular o Laplace de que, utilizando a tabela de transformadas de Laplace, será .
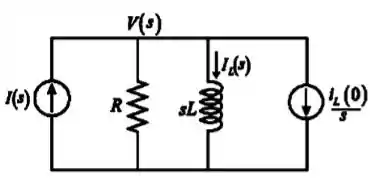
Então, vamos aqui desenhar esse circuito no domínio de Laplace (domínio s) pra ficar mais claro:
Passo 2
Aplicando a lei das correntes de Kirchhoff no circuito:
Além disso vamos substituir por chegando em:
Passo 3
Agora, podemos substituir todos os valores que temos dos elementos e também de e
Passo 4
Separando em frações parciais teremos:
Agora basta encontrar
Daí, substituindo, teremos:
Por Laplace utilizando a tabela de transformadas, teremos:
Resposta
Exercícios de Livros Relacionados
Não há nenhuma energia armazenada no circuito mostrado na Figura P12.27, no momento em que a chave é aberta. a) Deduza a equação íntegro-diferencial que governa o comportamento da tensão vo. b) Mostre
a) Use o teorema do valor inicial para determinar o valor inicial de v no Problema 12.26. b) O teorema do valor final pode ser usado para determinar o valor de regime permanente de v? Por quê?
a) Deduza o par de transformadas dado pela Equação 12.83. b) Deduza o par de transformadas dado pela Equação 12.84.
Não há nenhuma energia armazenada no circuito mostrado na Figura P12.31, no momento em que a chave é aberta. a) Deduza a equação íntegro-diferencial que governa o comportamento das tensões de nó v1 e
Mostre que, se F s = L f t e f t / t possuir transformada de Laplace, então ∫ s ∞ F u d u = L f t t . (Sugestão: use a equação que define a transformada de Laplace para escrever q s F(u)du = q s a q 0