Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 6.Problemas - Ex. 56
Determine a em cada um dos circuitos da figura 6.78.
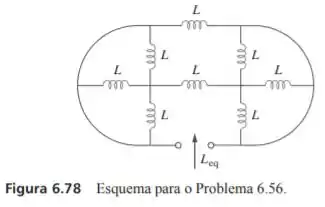
Passo 1
Devemos lembrar ainda que a regra que vale para os indutores é igual a regra que vale para os resistores ou seja
Onde representa uma associação em série e associação em paralelo. Porém, vamos reescrever o circuito de uma forma mais simples de modo a facilitar nossa interpretação
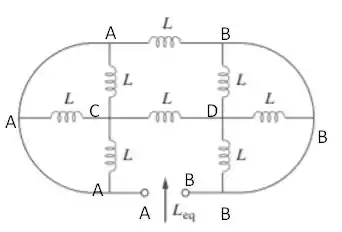
Reescrevendo esse circuito vamos obter
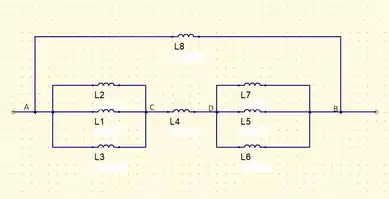
Para os que estão associado em paralelo vamos ter como indutor resultante que estarão associados em série com . Dessa forma, iremos obter
Por fim, para concluirmos o exercício vamos ter uma última associação em paralelo entre e o resultante calculado acima. Portanto, temos
Resposta
Exercícios de Livros Relacionados
Se v 0 - = 2,5V , calcule i ( 0 + ) e d i 0 + / d t.
Se v(0-) = 12 V, calcule wL (0+) e di(0+)/dt
Determine o circuito dual para a rede de:a) b) c)
Se o circuito está em regime permanente em t = 0 - . Calcule d v d te d i d t em t = 0 + .
Se v 0 - = 10V , calcule w L 0 + e d i 0 + d t .