Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 6.Problemas - Ex. 57

Determine a L e q que pode ser usada para representar o circuito indutivo da figura 6.79 nos terminais.

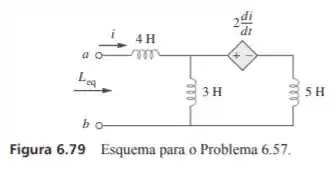
Passo 1

Da equação padrão dos indutores nós temos que

v = L e q ⋅ d i d t     i

A partir do nosso circuito observando os seus indutores pode inferir as seguintes equações

v = v 1 + v 2 = 4 ⋅ d i d t + v 2     i i

i = i 1 + i 2 → i 2 = i - i 1     i i i

v 2 = 3 ⋅ d i 1 d t → v 2 3 = d i 1 d t       i v

Aplicando a lei das malhas no nosso circuito vamos achar

- v 2 + 2 ⋅ d i d t + 5 ⋅ d i 2 d t = 0       v

Passo 2

Com as equações acima em mãos podemos substituir i i i   e   ( i v ) em v , obtendo assim

v 2 = 2 ⋅ d i d t + 5 ⋅ d i - i 1 d t → v 2 = 2 ⋅ d i d t + 5 ⋅ d i d t - 5 d i 1 d t

v 2 = 7 ⋅ d i d t - 5 3 ⋅ v 2 → v 2 ⋅ 1 + 5 3 = 7 ⋅ d i d t → 8 v 2 3 = 7 ⋅ d i d t → v 2 = 21 8 ⋅ d i d t     v i

Substituindo v i   e m   i i teremos

v = 4 ⋅ d i d t + 21 8 ⋅ d i d t → v = 53 8 ⋅ d i d t

Através da comparação com a equação i vamos encontrar que

L e q = 53 8   H

Resposta

L e q = 53 8   H

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Deduza uma equação para a divisão da tensão entre os dois indutores em série, por meio de V1 e V2.
0 circuito está em est ado permanente cc em t = 0-. Calcule (a) Vo (b) iv (c) i e (d) iR em t = 0- e em t = 0+
Se o circuito está em estado permanente cc em t = 0-, calcule (a) i1 (b) il e (c) vL em t = 0- e em t = 0+
Construa circuitos duais para as redes de (a) Fig. 7.4, (b) Fig. 7.10, (c) Fig. 7.12 e (d) Fig. 7.15. Fig 7.4 Fig 7.10Fig 7.12 Fig 7.15
Na Fig. 7.18, considere L1 = 4 H, L2 = 2H, i1(0-) = 3 A, i2(0-) = 6 A, e caIcule i1(0+), i2(0+), e a energia total armazenada no circuito em t = 0- e em t = 0+.