Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 7.Problemas - Ex. 25
Se , calcule e .
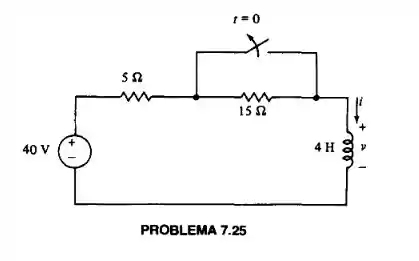
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Pelo enunciado, nós temos que , essa informação para fazer LKT, já que a malha continua fechada, logo
Substituindo o , nós obtemos o seguinte resultado
Logo
Analisamos o circuito para , só que para o indutor, a corrente não pode variar instantaneamente, com isso, temos a relação
E depende dos fatores do indutor, com isso, já podemos calcular
Que será igual a
Passo 2
Para a derivada, vamos ter que refazer a LKT para , o que não muda muita coisa, para nossa alegria (lembra do meme? Rsrsrs)
Lembrando que é a tensão no indutor, então podemos modificar e brincar um pouco com essa LKT, portanto
Substituindo os valores, nós temos que