Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 41
41. Determine no circuito da figura supondo que
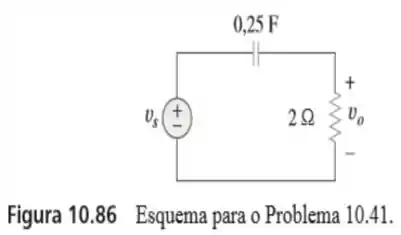
Passo 1
Fala galerinha! Bora pro nosso segundo probleminha sobre superposição em circuitos .
Olha só! Nesse tipo de problema, há a presença de apenas uma fonte de tensão alternada. Só que o problema é que essa fonte está em duas frequência diferentes, e .
O que precisamos fazer pra esse caso, é considerar essa fonte como se ela fosse dividida em duas... Uma fonte de tensão alternada com uma frequência de e outra fonte de corrente alternada com frequência de , que chamaremos de e , respectivamente.
Depois, vamos somar essas fontes.
Vamos então, por a mão na massa.
Passo 2
Primeiramente, vamos considerar apenas a fonte , excluindo a fonte com frequência de .
Antes, vamos passar os elementos pro domínio da frequência:
Desse modo, o nosso circuito vai ficar com a seguinte cara:
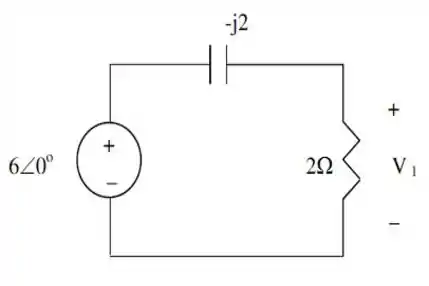
Por divisão de tensão, o valor de é dado por:
Passando para o domínio do tempo:
Passo 3
Agora, vamos excluir a fonte de tensão alternada com frequência de e considerar apenas .
E já sabe, né! Primeira coisa a se fazer é passar os elementos pro domínio da frequência:
Desse jeito, o nosso circuito passa a ser representado pela seguinte figura:
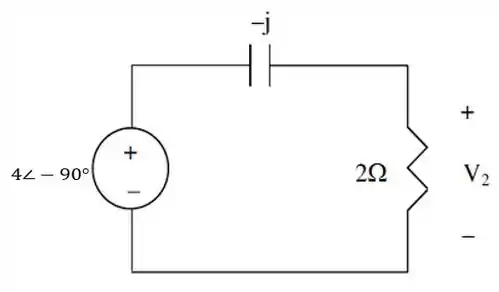
E novamente fazendo uso da divisão de tensão, temos que o valor de é dado por:
Passando pro domínio do tempo...
Para fazer passar de uma função cosseno para uma função seno, basta somar de ângulo:
Conseguimos o que queríamos!
Passo 4
Pra finalizar, basta somar as tensões e e iremos obter :
Pronto! Missão cumprida!