Enunciado
Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 5.3 - Ex. 3
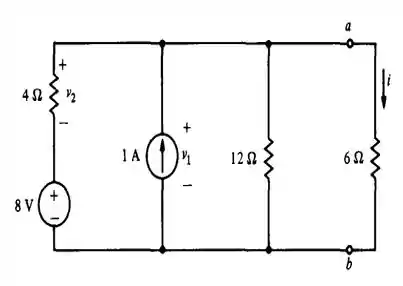
Substitua tudo no circuito do Ex. 5.3.1, exceto o resistor de , pelo seu equivalente de Norton e use o resultado para calcular .
Passo 1
Primeiro passo é calcular a resistência Thévenin. Para isso, vamos substituir todas as fontes de tensão por curto circuitos:
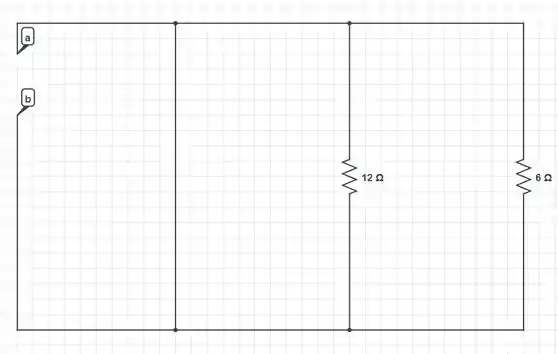
Podemos ver que em relação aos terminais e , os resistores estão em paralelo. Logo:
Passo 2
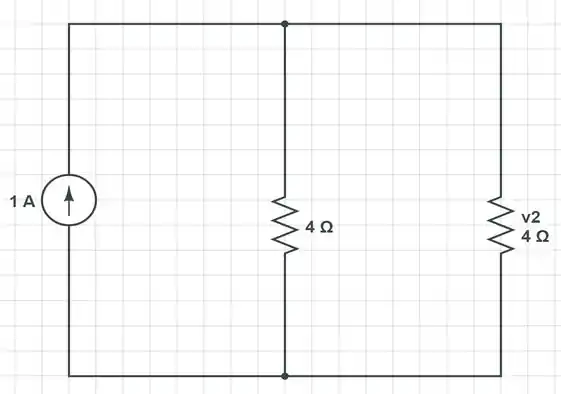
Para calcular a tensão de Thévenin, vamos manter o circuito em aberto entre os pontos A e B, enquanto retornamos com as duas fontes de tensão:
Dessa forma, usando o método do divisor de tensão chegamos à...
Para calcular a fonte de corrente para o equivalente Norton, devemos dividir a tensão de Thévenin pela resistência Thévenin:
E sabemos que a resistência Norton é igual a resistência Thévenin:
Passo 3
Dessa forma, ficamos com o seguinte circuito de Norton...
A questão final aqui é achar a tensão naquele resistor!
Bom! Usando o método do divisor de corrente, a corrente que vai estar circulando nele será de...
Isso então, vai nos dar uma tensão de...
Pronto! Finalizamos aqui!