Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 13.Problemas - Ex. 3
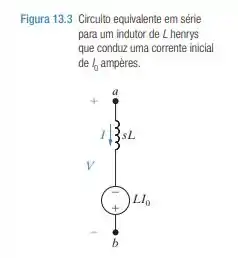
Determine o equivalente de Norton do circuito da Figura 13.3.
Passo 1
Falaaa, pessoal! Como vocês estão?
Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre transformada de Laplace na análise de circuitos!
Podemos determinar o equivalente de Norton do sistema mostrado na figura acima pela seguinte expressão, por definição:
Passo 2
Ou seja, temos:
Dessa forma, podemos concluir que o equivalente de Norton é o mesmo do circuito da Fig. 13.4, abordada na questão 13.1.
Resposta
O equivalente de Norton é o mesmo do circuito da Fig. 13.4, abordada na questão 13.1.
Exercícios de Livros Relacionados
Determine os polos e zeros da impedância vista a partir dos terminais a,b do circuito da Figura P13.8.
A chave no circuito da Figura P13.13 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente de a para b. a) Construa um circuito no domínio da frequência, para t0. b) Determine V
a) Determine a expressão de V o no domínio da frequência, para o circuito da Figura P13.17. b) Use a expressão no domínio da frequência determinada em (a) para prever os valores inicial e final de v o
A chave no circuito da Figura P13.12 esteve fechada por um longo tempo. Em t = 0, ela é aberta. a) Determine i o, para t $ 0. b) Determine vo, para t $ 0. b) Determine vo, para t $ 0.
Não há nenhuma energia armazenada no circuito da Figura P13.22, em t = 0-. a) Determine Vo. b) Determine vo. c) A solução para vo faz sentido em termos do comportamento conhecido do circuito? Explique