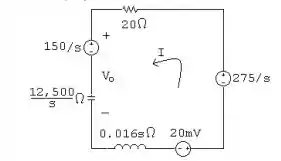
A chave no circuito da Figura P13.13 esteve na posição a por um longo tempo. Em t = 0, ela passa instantaneamente de a para b.
a) Construa um circuito no domínio da frequência, para t > 0.
b) Determine .
c) Determine .

Passo 1
Falaaa, pessoal! Como vocês estão?
Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre transformada de Laplace na análise de circuitos!
- Quando existe essa condição, podemos demonstrar o circuito através da ilustração abaixo:
- Para , fazemos a seguinte conta:
- Para encontrar , começamos definindo o valor de cada componente de K para chegarmos na expressão correta, tendo então:
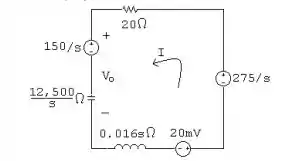
Fazendo e desenvolvendo a equação, temos que:
Juntando com a primeira conta:
Passo 2
Temos então que:
Por fim:
Resposta
- Item a:
- Item b:
- Item c: