Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 15
Determine o equivalente de Norton para o circuito da Figura 13.84 nos terminais a-b.
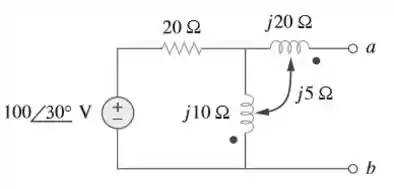
Passo 1
Vamos lá galera! O primeiro passo é substituir os circuitos mutuamente acoplados pelos circuitos equivalentes usando fontes dependentes. Para obter , fazemos um curto-circuito a – b como mostrado na figura abaixo e resolvemos isolando
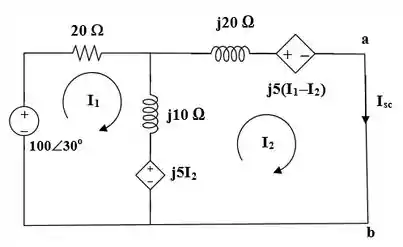
Passo 2
Legal? Agora tudo que precisamos fazer é escrever as duas equações das nossas malhas!
Malha 1,
Malha 2,
Subnstituindo na equação novamente, temos:
Resolvendo para
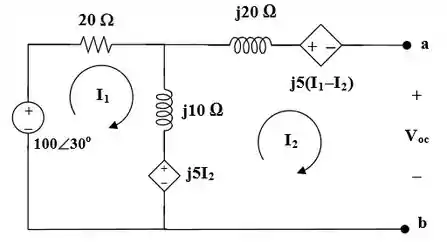
Passo 3
Para resolver , tudo o que precisamos fazer é resolver o . No circuito acima, observamos que e obtemos a equação da malha, ou (tensão induzida devido ao acoplamento mútuo) = .
Portanto,
Resposta
Exercícios de Livros Relacionados
Para as três bobinas acopladas da Figura 13.72, calcule a indutância total.
Considere a figura 13.73 e elabore um problema para ajudar outros estudantes a entender melhor a indutância mútua.
Duas bobinas ligadas de forma a favorecer a conexão em série possuem indutância total de 500m H . Quando ligadas em uma configuração de forma a se opor à conexão em série, as bobinas apresentam uma in
Duas bobinas estão acopladas mutuamente, com L 1=50m H , L 2=120m Hek=0,5 . Calcule a máxima indutância possível se:As duas bobinas estiverem conectadas em sérieAs duas bobibnas estiverem conectadas e