Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 1
Para as três bobinas acopladas da Figura 13.72, calcule a indutância total.
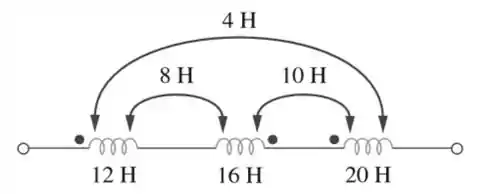
Passo 1
Certo pessoal vamos lá! Essa questão exige um pouquinho de atenção a mais, mas não se procupem! Primeiramente temos que nos atentar para a posição dos enrolamentos nas bobibas. Considerando o indutor de como referência, temos que:
Para a bobina 1,
Para a bobina 2,
Para a bobina 3,
Passo 2
Agora basta somarmos as indutâncias já calculadas com as indutâncias mutuas para achar a inutancia total!
Resposta
Exercícios de Livros Relacionados
Considere a figura 13.73 e elabore um problema para ajudar outros estudantes a entender melhor a indutância mútua.
Duas bobinas ligadas de forma a favorecer a conexão em série possuem indutância total de 500m H . Quando ligadas em uma configuração de forma a se opor à conexão em série, as bobinas apresentam uma in
Duas bobinas estão acopladas mutuamente, com L 1=50m H , L 2=120m Hek=0,5 . Calcule a máxima indutância possível se:As duas bobinas estiverem conectadas em sérieAs duas bobibnas estiverem conectadas e
Para as bobinas acopladas na Figura 13.74a, demonstre que L e q = L 1 + L 2 + 2 M Para as bobinas acopladas na Figura 13.74b demonstre que L e q = L 1 L 2 - M 2 L 1 + L 2 - 2 M
As bobinas na Figura 13.75 têm L 1 = 40m H , L 2 = 5m H e coeficiente de acoplamento k =0 , 6 . Determine i 1 ( t ) e v 2 ( t ) dado que v 1 ( t ) = 20c o sv t e i 2 ( t ) = 4s e nv t , v=2.000r a d /