Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 16
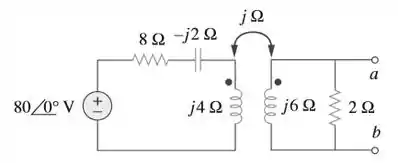
Obtenha o equivalente de Norton nos terminais a-b do circuito da Figura 13.85
Passo 1
Vamos lá galera! O primeiro passo é curto circuitar os terminais a-b. Para termos 2 malhas e trabalharmos em cima delas.
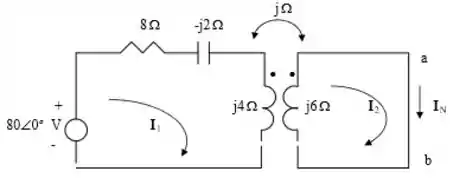
Resolvendo esse sistema, temos:
Passo 2
Legal? Para acharmos a impedância, temos que inserir uma fonte de corrente de 1 A nos terminais a-b, como na figura abaixo.
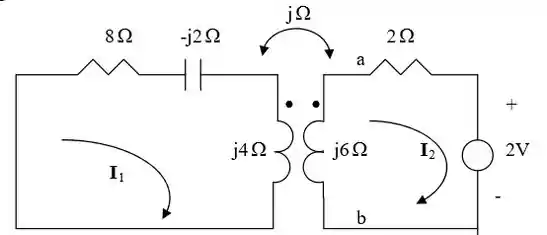
Passo 3
Das malhas, temos que:
Resposta
Exercícios de Livros Relacionados
Para as bobinas acopladas na Figura 13.74a, demonstre que L e q = L 1 + L 2 + 2 M Para as bobinas acopladas na Figura 13.74b demonstre que L e q = L 1 L 2 - M 2 L 1 + L 2 - 2 M
As bobinas na Figura 13.75 têm L 1 = 40m H , L 2 = 5m H e coeficiente de acoplamento k =0 , 6 . Determine i 1 ( t ) e v 2 ( t ) dado que v 1 ( t ) = 20c o sv t e i 2 ( t ) = 4s e nv t , v=2.000r a d /
Considere o circuito da Figura 13.76 e determine V o .
Determine v ( t ) para o circuito da Figura 13.77.
Determine V x no circuito da Figura 13.78.