Determine o equivalente de Thévenin à esquerda da carga no circuito da figura abaixo.
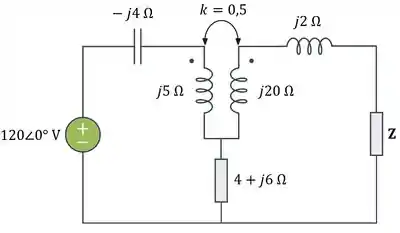
Passo 1
Vamos começar substituindo o circuito acoplado mutuamente pela fonte dependente equivalente. Primeiro determinaremos as tensões induzidas e, em seguida, definimos os sinais adequados.
A corrente induz uma tensão na segunda bobina representada pelo valor , e induz uma tensão de na primeira bobina. Sabemos:
e
Com a relação de indutância mútua, obtemos o valor de :
Portanto, a tensão induzida na segunda bobina é e na primeira bobina é .
Passo 2
Agora que já sabemos os valores das tensões induzidas, vamos determinar os sinais corretos para as fontes dependentes. A corrente entra em pelo lado do ponto e induz uma tensão em com um sinal + no lado superior e um sinal – no lado inferior. sai pela extremidade do ponto de induzindo uma tensão em com um sinal + no lado inferior e um sinal – no lado superior.
Então o circuito equivalente com as fonte dependentes é mostrado a seguir:
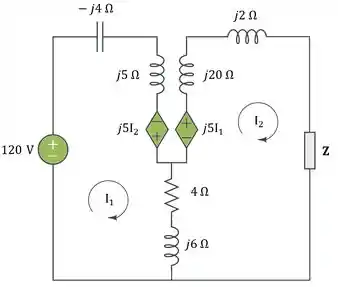
Passo 3
Consideremos o circuito abaixo para determinar :
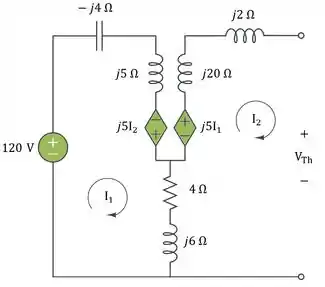
Para calcular a tensão do circuito aberto, notamos que é igual a zero. Aplicando a análise de
malhas aos dois laços, obtemos:
Vamos converter o denominador da fração para forma polar e assim facilitar nossa divisão:
Então a corrente será:
Agora que já sabemos a corrente, podemos calcular a tensão de circuito aberto:
Vamos converter novamente para forma polar afim de facilitar agora nossa multiplicação:
Assim, é calculada como se segue:
Passo 4
Vamos agora encontrar a impedância de entrada . Para isso vamos primeiro encontrar a corrente de curto-circuito do teorema de Norton, para assim calcular pela relação:
Então vamos lá! Para determinar curto-circuitamos os terminais de :
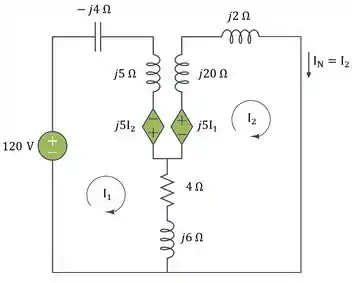
Resolvemos as seguintes equações de malha:
Malha 1:
Malha 2:
Convertendo da forma retangular para a polar:
Calculamos o valor de :
Substitiundo esse valor da equação da Malha 1, temos:
Sendo
Temos
Convertendo de polar para retangular e substituindo na equação:
Daí a gente volta a converter para forma polar e assim obtemos que é a corrente de curto-circuito :
Passo 5
Agora encontramos a impedância de entrada :
Resposta
Logo, o equivalente de Thévenin à esquerda da carga no circuito é:
e