Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 17
No circuito da figura abaixo, é um indutor de com impedância de . Determine quando .
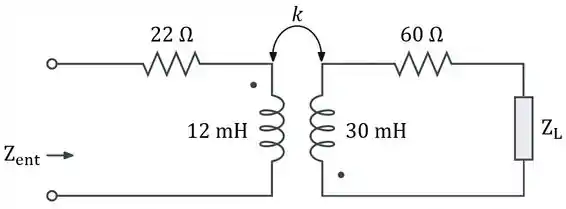
Passo 1
Vamos começar calculando a frequência angular . O valor de será usado mais tarde para determinar o circuito equivalente no domínio da frequência. A partir do valor de podemos calcular , já que , então:
Substituindo , temos:
Passo 2
Sabemos que o coeficiente de acoplamento é indicando que os indutores estão firmemente acoplados. Sendo e , com o valor de calculamos a indutância mútua :
Passo 3
Para determinar a impedância de entrada , precisamos obter o equivalente no domínio da frequência do circuito.
A impedância complexa de um indutor é dada por:
Sabemos que
e
Então, no domínio da frequência teremos:
Assim, o circuito equivalente é mostrado abaixo:
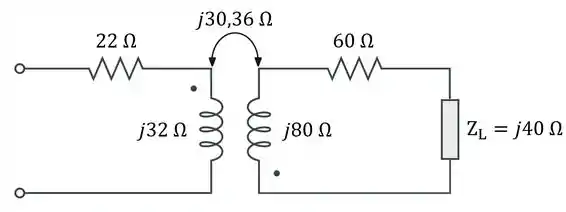
Passo 4
Obtemos a impedância de entrada, como segue:
Vamos converter o denominador da fração para forma polar e assim facilitar nossa divisão:
Assim, temos:
Feita a divisão, voltamos para forma polar:
E assim, determinamos a impedância de entrada:
Resposta
Logo, a impedância de entrada é: