Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 59
Determine a largura de banda e a frequência de corte do filtro rejeita-faixa da Figura 14.89.
Passo 1
O circuito é o observado abaixo já com os componentes nas suas respectivas impedâncias
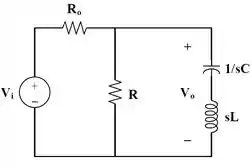
Neste foi dado os valores de
Passo 2
Vamos determinar a impedância total do circuito definida como Primeiro vamos encontrar composto pela associação em série do capacitor com indutor
Em seguida esta associação estará em paralelo com o resistor , logo
Multiplicando em cima e em baixo por
Passo 3
Logo a função de transferência será
Substituindo
Para que seja possível simplificar vamos multiplicar pelo denominador de isso será igual a
Para
Passo 4
Podemos ainda encontrar a frequência de ressonância por meio da equação
Como possuímos o valor de e C
Passo 5
O valor máximo da função de transferência é encontrado a frequência zero, logo
Ou quando a frequência tende ao infinito
Passo 6
Para encontrar e . Vamos partir do modulo da função e transferência, de modo que
Então
O numerado do lado esquerdo possui apenas números reais logo é necessário tirar o modulo apenas do denominador que contem componentes complexas
Isolando
O passo seguinte é substituir os valores dos componentes e fazer a multiplicação cruzada.
Colocando tudo sobre o mesmo denominador
Elevando tudo ao quadrado
Como a parcela pode ser subtraída dos dois lados ficamos com
Depois de toda essa álgebra, vamos abrir o produto e ficar com.
Que sendo dividido por é
Passo 7
O este polinômio encontraremos no mínimo 4 raízes, contudo só precisaremos de duas, e as duas positivas, já que não há frequência negativa
Chamaremos , logo
Dessa forma nossa equação de quarta ordem vira uma equação de 2 ordem, e essa sai ...
Para encontrar basta usar a raiz positiva de
Para encontrar basta usar a raiz positiva de
E a largura de banda é calculada por